$1.4.7^*.$ Какой будет продолжительность полета самолета из Новосибирска в Москву и обратно, происходящего по прямой, если в течение всего полета ветер дует под углом $\alpha$ к трассе со скоростью $u$? Скорость самолета относительно воздуха $v$, длина трассы $L$. При каком направлении ветра продолжительность полета максимальна?
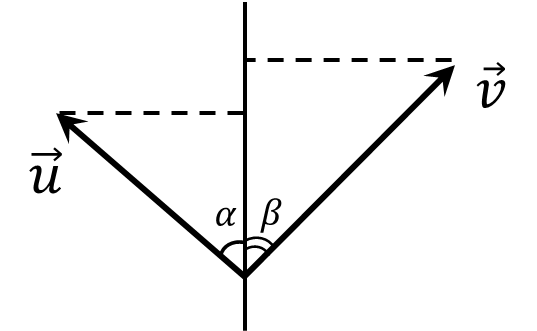
Чтобы самолет летел по курсу необходимо, чтобы выполнялось условие
$u \sin\alpha = v \sin\beta$
Откуда
$\cos\beta = \sqrt{1 - u^2 \sin^2 \alpha / v^2}$
А полное время туда и обратно
$$t_1 = \frac{L}{v \cos\beta + u \cos\alpha}$$
$$t_2 = \frac{L}{v\cos\beta - u \cos\alpha}$$
Полное время найдем, как
$t=t_1+t_2$
Подставим значение $\cos\beta$:
$$t=\frac{L}{\sqrt{v^2 - u^2 \sin^2 \alpha} + u \cos\alpha} + \frac{L}{\sqrt{v^2 - u^2 \sin^2 \alpha} - u \cos\alpha}$$
$$t=L\frac{\sqrt{v^2 - u^2 \sin^2 \alpha}+\sqrt{v^2 - u^2 \sin^2 \alpha} }{(\sqrt{v^2 - u^2 \sin^2 \alpha} + u \cos\alpha )(\sqrt{v^2 - u^2 \sin^2 \alpha} - u \cos\alpha )}$$
$$t=\frac{2L\sqrt{v^2 - u^2 \sin^2 \alpha}}{(\sqrt{v^2 - u^2 \sin^2 \alpha} + u \cos\alpha )(\sqrt{v^2 - u^2 \sin^2 \alpha} - u \cos\alpha )}$$
Выражаем искомое время:
$$\fbox{$t=\frac{2L\sqrt{v^2 - u^2 \sin^2 \alpha}}{v^{2}-u^{2}}$}$$
$$t=\frac{2L\sqrt{v^{2}-u^{2}\operatorname{sin}^{2}\alpha}}{v^{2}-u^{2}}.\textrm{ Вдоль трассы}.$$