Условие:

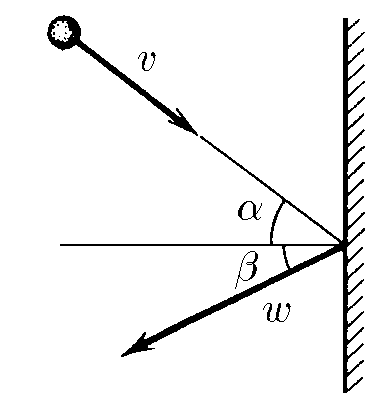
$1.4.9.$ Тело налетает на стенку со скоростью $v$ пол углом $\alpha$ к линии, перпендикулярной стенке. Определите скорость тела после упругого удара, если стенка:

а) неподвижна;

б) движется перпендикулярно самой себе со скоростью $w$ навстречу телу;

в) движется под углом $\beta$ к линии, перпендикулярной ей самой, со скоростью $w$ навстречу телу

Решение:

$а)$ Т.к. соударение упругое, то по Закону Сохранения Импульса:

$v \sin\alpha = u \sin\alpha$

$\fbox{$v = u $}$

$б)$ Далее эта задача немного напоминает 1.4.8.

В системе отсчета связанной со стенкой относительная скорость шарика $\vec{v_{отн}} = \vec{v} - \vec{w}$. При упругом отражении, переходя в СО земли скорость равняется $\vec{u} = \vec{v} - 2\vec{w}$.

Ниже наглядно продемонстрирована работа с векторными величинами

Иллюстрация скоростей шарика

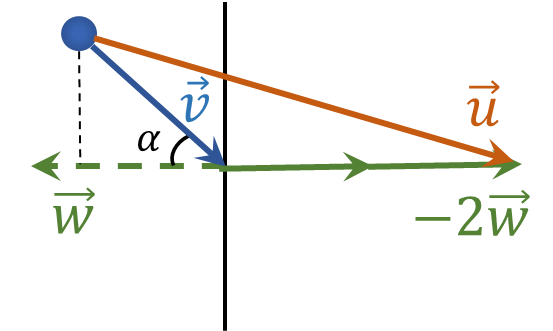
Найдем проекции вектора $\vec{u}$ на горизонтальную и вертикальные оси:

$u_y = v \sin\alpha$

$u_x = v \cos\alpha + 2w$

Воспользовывшись т. Пифагора, найдем модуль вектора $\vec{u}$

$u = \sqrt{u_x^2+u_y^2}$

$u = \sqrt{(v \sin\alpha )^2 + (v \cos\alpha + 2w)^2}$

$\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha +4w^{2}}$}$

$в)$ Аналогично предыдущему подпункту

$\vec{u} = \vec{v} - 2\vec{w}$

Покажем эти вектора на рисунке

Иллюстрация скоростей шарика

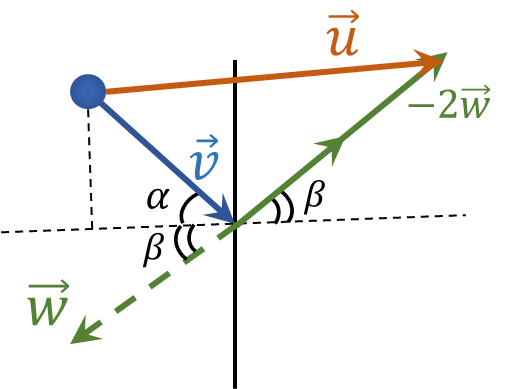
Найдем проекции вектора $\vec{u}$ на горизонтальную и вертикальные оси:

$u_y = v \sin\alpha - 2w \sin\beta$

$u_x = v \cos\alpha + 2w \cos\beta$

Воспользовывшись т. Пифагора, найдем модуль вектора $\vec{u}$

$u = \sqrt{u_x^2+u_y^2}$

$u = \sqrt{(v \sin\alpha - 2w \sin\beta )^2 + (v \cos\alpha + 2w \cos\beta )^2}$

$\fbox{$u=\sqrt{v^{2}+4vw\cos\alpha\cos\beta +4w^{2}\cos^{2}\beta}$}$

Ответ:

$\text{a) } u=v.\quad\text{б) } u=\sqrt{v^{2}+4vw\cos\alpha +4w^{2}}.\quad\text{в) } u=\sqrt{v^{2}+4vw\cos\alpha\cos\beta +4w^{2}\cos^{2}\beta}.$