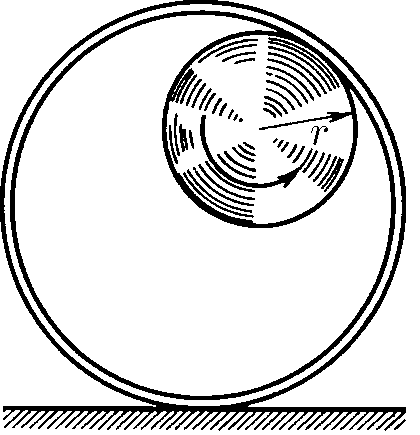
$1.5.10.$ По внутренней поверхности закрепленного цилиндра радиуса $2r$ катится без проскальзывания колесо радиуса $r$. Найдите траекторию точки обода колеса
Данная траектория является так называемой Гипоциклоидой Заданная параметричеким уравнением:
$$\begin{gathered}\begin{cases}x=r(k-1)\left(\cos t+\frac{\cos((k-1)t)}{k-1}\right)\\y=r(k-1)\left(\sin t-\frac{\sin((k-1)t)}{k-1}\right)&\end{cases}\end{gathered}$$
При $r= R/2$, данная траетория ложиться на диаметр
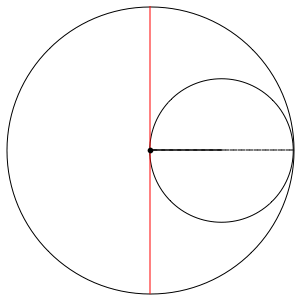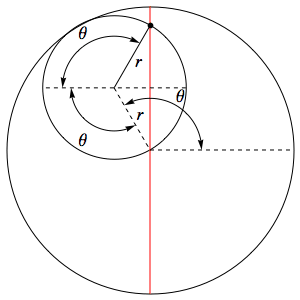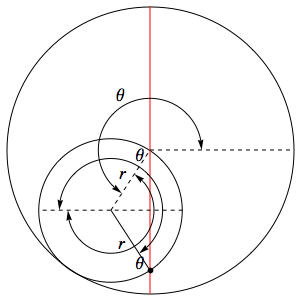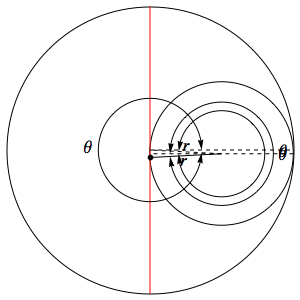
Пусть в начальный момент окружности касаются в точке $A$, лежащей на оси $Ox$, где точка $O$ — центр большой окружности. Координаты точки $A$ при этом - $ (kr, 0) $, где $ k = \frac{R}{r} $. Рассмотрим, как меняются координаты точки $A$, привязанной к катящейся окружности ($A$ переходит в $ A' $). Пусть маленькая окружность прокатилась так, что её центр перешел из точки $ C' $ в точку $ C'' $ и повернулся относительно точки $O$ на угол $ t $.
Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между $ CA $ и $ C' A' $) равен $ t - kt = -(k-1)t $. Во-вторых, координаты точки $ C' $ будут такими: $ (cos(t)(k-1)r, \sin(t)(k-1)r) $. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки $ A' $:
$ \begin{cases} x = \cos(t)(k-1)r + \cos((k-1)t)r \\ y = \sin(t)(k-1)r - \sin((k-1)t)r \end{cases} $
Траектория точки обода колеса проходит по диаметру цилиндра.