$1.5.12.$ Бусинка может двигаться по кольцу радиуса $R$, подталкиваемая спицей, равномерно вращающейся с угловой скоростью $\omega$ в плоскости кольца. Ось вращения спицы находится на кольце. Определите ускорение бусинки.
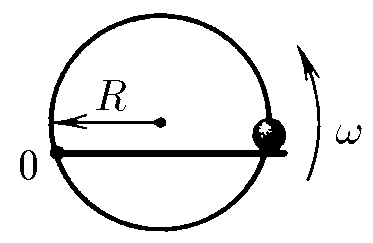
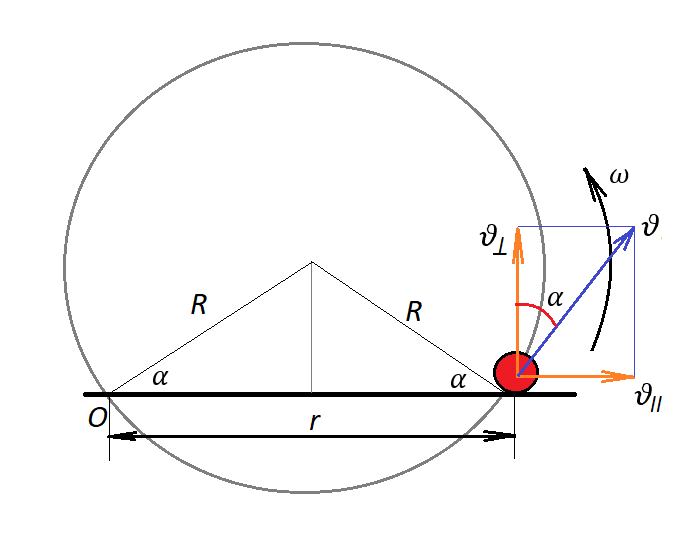
Бусинка будет двигаться вдоль спицы со скоростью $\upsilon_{\parallel}$, и, поскольку спица вращается, то у бусинки будет составляющая скорости, перпендикулярная спице: $\upsilon_{\perp}$
Тогда абсолютная скорость $\vec{v}$ в НСО, будет равна векторной сумме $\vec{v}_{отн}$ и $\vec{v}_{кл}$
$\upsilon_{\perp}=\omega r=\omega\cdot 2R\cos\alpha$
С другой стороны,
Тогда абсолютная скорость $\vec{v}$ в НСО, будет равна векторной сумме $\vec{v}_{отн}$ и $\vec{v}_{кл}$
$\upsilon_{\perp}=\upsilon\cos\alpha$
Так как скорость бусинки, движущейся по окружности, направлена перпендикулярно радиусу.
Тогда
$\omega\cdot 2R\cos\alpha =\upsilon\cos\alpha$
$\upsilon =2R\omega =\text{const}$
Так как скорость по модулю не меняется, то у бусинки есть только нормальное ускорение
$$a_n=\frac{\upsilon^2}{R}=\frac{4\omega^2R^2}{R}=4\omega^2R$$