$1.5.14^*.$ Четыре черепахи находятся в вершинах квадрата со стороной $a$. Они начинают двигаться одновременно с постоянной по модулю скоростью $v$. Каждая черепаха движется по направлению к своей соседке по часовой стрелке. Где встретятся черепахи и через какое время?
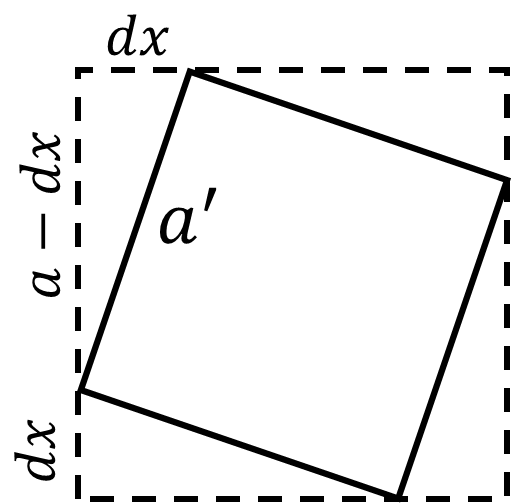
Рассмотрим изменение координат черепах за маленький промежуток времени $dt$
За время $dt$ расстояние между соседними черепахами изменилось с $a$ на $a'$
Выразим $a'$ по т.Пифагора
$a' = \sqrt{(a-dx)^2 - d^2x}$
С учетом малости величины $dx$
$a' = \sqrt{a^2 - 2a\, dx}$
$$a' = a\sqrt{1 - \frac{2dx}{a}}$$
Воспользуемся формулой для малых величин $(1+x)^\alpha\approx 1+\alpha x$, где $x\rightarrow 0$:
$a' = a - dx$
Таким образом, приращение координаты $a$ равно
$da = a' - a = dx$
Отсюда, скорость изменения расстояния между черепахами равна
$$u = \frac{da}{dt} = -\frac{dx}{dt}=-v$$
Отсюда следуеь, что через $a=0$, через промежуток времени
$t = a/v$
Из симметрии задачи, следует, что все черепахи пройдут одинаковый путь и окажутся в центе квадрата.
NO: Интересно было бы узнать, что было бы если был бы не квадрат? Если было бы не $4$ черепахи, а $n$ штук? Более развернутую версию задачи можно найти в "Очень длинных физических задачах" А.И.Слободянюка(Задача 1)
В центре квадрата через время $t = a/v$.