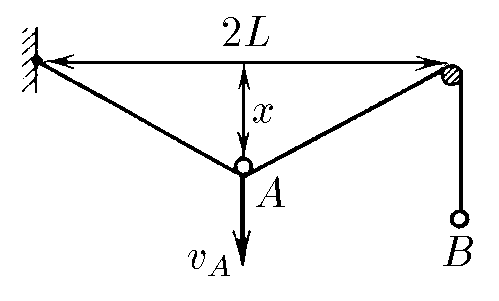
$ 1.5.15.$ Постройте примерный график зависимости скорости точки $B$ от времени, если скорость $v_{a}$ точки $A$ постоянна. Найдите формулу этой зависимости, если $x(0) = 0$.

NO: Перед просмотром решения данной задачи, советую ознакомиться с решением 1.5.14
В момент времени $t$ высота, на которую опустилась точка
$$x = v_A t\quad(1)$$
Рассмотрим изменение длины нити за маленький промежуток времени $dt$
$$dl = \sqrt{L^2 + (x+dx)^2}-\sqrt{L^2 + x^2}$$
$$dl = \sqrt{L^2 + x^2}(\sqrt{1 + \frac{2xdx}{L^2 + x^2}}-1)$$
Воспользуемся формулой для малых величин $(1+x)^\alpha\approx 1+\alpha x$, где $x\rightarrow 0$:
$$dl = \frac{xdx}{\sqrt{L^2 + x^2}}$$
Учитывая, что $v_B = \frac{dl}{dt}$ и $v_A = \frac{dx}{dt}$
$$v_B = \frac{x}{\sqrt{L^2 + x^2}} \frac{dx}{dt}$$
$$v_B = v_A\frac{x}{\sqrt{L^2 + x^2}}$$
Подставляем $(1):$
$$\fbox{$v_B = \frac{v_A^2t}{\sqrt{L^2 + v_A^2t^2}}$}$$
NO: Более развернутую и красивую задачу с похожей идеей можно найти в "Очень длинных физических задачах" А.И.Слободянюка(Задача 2)