$ 1.5.16.$ Стержень упирается своими концами в стороны прямого угла. Верхний конец стержня поднимают со скоростью $v$. Найдите, как зависит от времени скорость его нижнего конца. За начало отсчета времени принять момент, когда верхний конец находится в вершине угла. Длина стержня $L$.
NO: Перед просмотром решения данной задачи, советую ознакомиться с решением 1.5.14 и 1.5.15
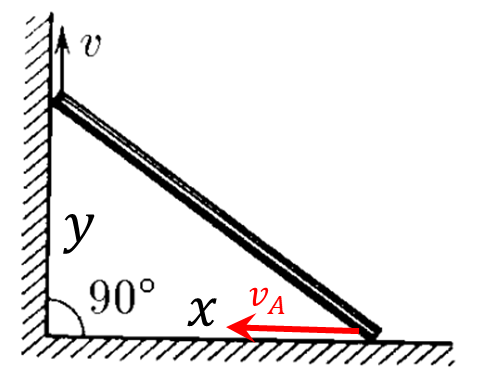
В момент времени $t$ высота, на которую поднялся верхний конец
$$y = v t\quad(1)$$
Рассмотрим изменение координаты $x = \sqrt{L^2-y^2}$ за малый промежуток времени $dt$
$$dx = \frac{ydy}{\sqrt{L^2 - y^2}}$$
Учитывая, что $v = \frac{dy}{dt}$ и $v_A = \frac{dx}{dt}$
$$v_A = \frac{vy}{\sqrt{L^2 - y^2}}$$
Подставляем $(1)$
$$\fbox{$v_A = \frac{v^2t}{\sqrt{L^2 - v^2t^2}}$}$$
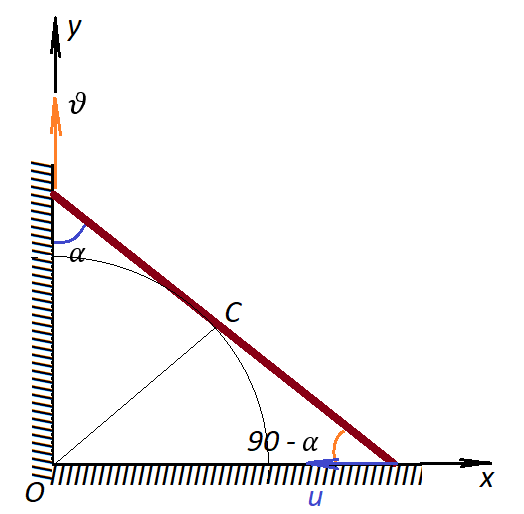
Координата верхнего конца может быть найдена как
$$y=\upsilon t$$
Проекции скоростей обоих концов на направление стержня равны:
$$\upsilon\cos\alpha =u\cos(90^{\circ}-\alpha )$$
$$\upsilon\cos\alpha =u\sin\alpha$$
$$u=\upsilon\operatorname{ctg}\alpha =\upsilon\frac{y}{x}$$
По теореме Пифагора
$$x^2+y^2=L^2$$
$$x=\sqrt{L^2-y^2}=\sqrt{L^2-\upsilon^2t^2}$$
Так как скорость $u$ направлена против оси $x$, то
$$x’=-u$$
$$u=-\frac{\frac{1}{2}\cdot 2t\cdot (-\upsilon^2)}{\sqrt{L^2-\upsilon^2t^2}}$$
$$u=\frac{t\cdot \upsilon^2}{\sqrt{L^2-\upsilon^2t^2}}$$
Если соединить центр стержня с вершиной прямого угла, то этот отрезок будет медианой прямоугольного треугольника и равен будет половине длины гипотенузы. Получается, что центр стержня движется по окружности с центром в точке О.