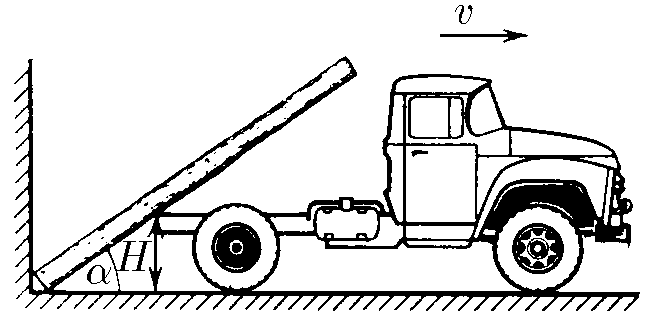
$ 1.5.17.$ Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте $H$ от земли. Найдите угловую скорость бревна в зависимости от угла $\alpha$ между ним и горизонталью, если грузовик отъезжает от стены со скоростью $v$.
NO: Перед просмотром решения данной задачи, советую ознакомиться с решением 1.5.16
В момент времени $t$ автомобиль проедет расстояние путь $vt$ и дно будет иметь горизонатальную координату $x$
$$x = H \tan\alpha\quad(1)$$
Рассмотрим изменение угла $\alpha = \arctan \frac{H}{x}$ за малый промежуток времени $dt$
$$d\alpha = d(\arctan \frac{H}{x})$$
$$d\alpha = \frac{1}{1+\frac{H^2}{x^2}} \frac{H}{x^2}$$
$$d\alpha = dx\frac{H}{x^2+H^2}$$
Учитывая, что $\omega = \frac{d \alpha}{dt}$ и $v = \frac{dx}{dt}$
$$\omega = \frac{vH}{x^2+H^2}$$
Подставляем $(1)$
$$\omega = \frac{v}{H(1 + \tan^2 \alpha )}$$
$$\fbox{$\omega = \frac{v \sin^2 \alpha}{H}$}$$
За время $\Delta t$ грузовик отъедет на расстояние
$$\Delta l=\upsilon\Delta t$$
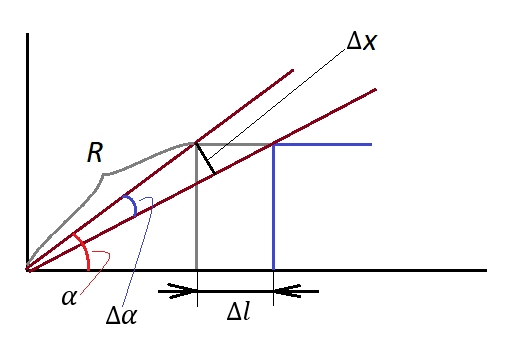
При этом бревно чуть опустится, повернувшись на малый угол $\Delta \alpha$. Если длина дуги поворота $\Delta x$, то по определению радианной меры угла
$$\Delta \alpha =\frac{\Delta x }{R}$$
Угловая скорость определяется как
$$\omega =\frac{\Delta \alpha}{\Delta t }=\frac{\Delta x }{R\Delta t }$$
Но $\Delta x =\upsilon\Delta t\sin\alpha$.
$$\omega =\frac{\upsilon\Delta t\sin\alpha}{R\Delta t }=\frac{\upsilon\sin\alpha}{R}$$
Также можно записать, что
$$H=R\sin\alpha$$
С учетом этого
$$\omega =\frac{\upsilon\sin^2 \alpha}{H}$$