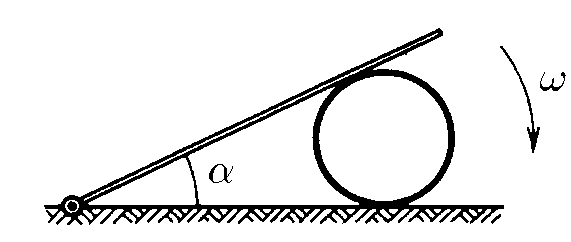
$ 1.5.18^*.$ Стержень, одним концом шарнирно закрепленный на горизонтальной плоскости, лежит на цилиндре. Угловая скорость стержня $\omega$. Проскальзывания между цилиндром и плоскостью нет. Найдите зависимость угловой скорости цилиндра от угла $\alpha$ между стержнем и плоскостью.
NO: Перед просмотром решения данной задачи, советую ознакомиться с решением 1.5.17
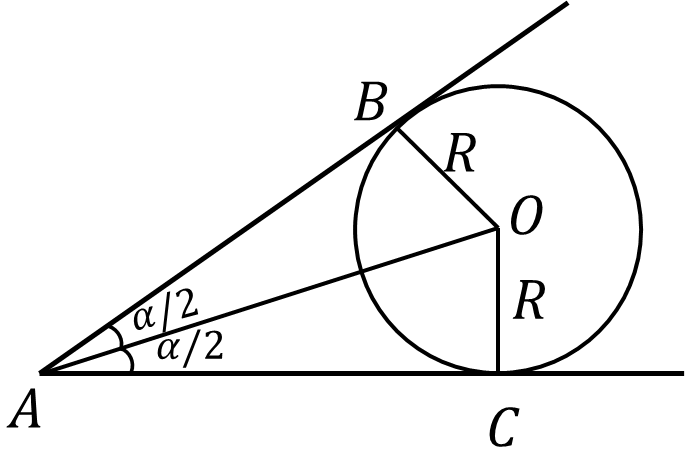
К моменту времени $t$ стержень будет составлять угол $\alpha$
Рассмотрим изменение координаты $x = AC$ за малый промежуток времени $dt$
$$dx = d(\frac{R}{\tan (\frac{\alpha}{2})})$$
Делим обе части на $dt$
$$\frac{dx}{dt} = \frac{d(\frac{R}{\tan\alpha /2})}{dt}$$
Учитывая, что $\omega = \frac{d \alpha}{dt}$ и $v = \frac{dx}{dt}$
$$v = \frac{\omega R}{2 \sin^2 (\frac{\alpha}{2})} $$
Запишем условие отсутсвия проскальзывания
$$\omega ' R = v$$
Отсюда
$$\fbox{$\omega ' = \frac{\omega}{2 \sin^2 (\frac{\alpha}{2})}$}$$