$ 1.5.19.$ Сферический буй радиуса $R$ привязан ко дну водоема. Уровень воды в водоеме поднимается со скоростью $u$. Какова скорость перемещения границы затопленной части буя по его поверхности в момент, когда уровень воды оказывается на $h$ выше центра буя?
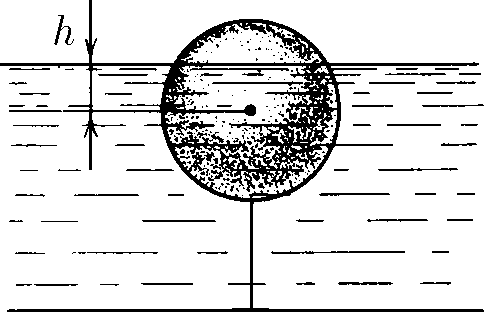
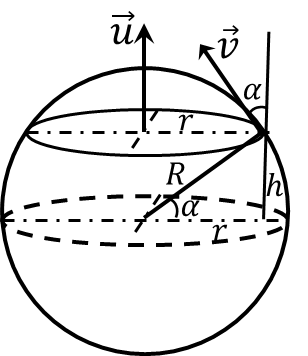
К моменту времени $t$ уровень воды будет составлять $h$
За маленький промежуток времени $dt$ слой воды поднимиться на
$$dh = u \, dt$$
В свою очередь граница затопленной части также поднимется на
$$dh = v\, dt \cos\alpha$$
Приравниваем оба уравнения
$$v \cos\alpha = u$$
$$v = \frac{u}{\cos\alpha}$$
$$\fbox{$v = u \frac{R}{\sqrt{R^2 - h^2}}$}$$