$ 1.5.20.$ Бобина магнитофонной пленки проигрывается в течение времени $t$ при скорости протяжки пленки $v$. Начальный радиус бобины (с пленкой) равен $R$, а конечный (без пленки) — $r$. Какова толщина пленки?
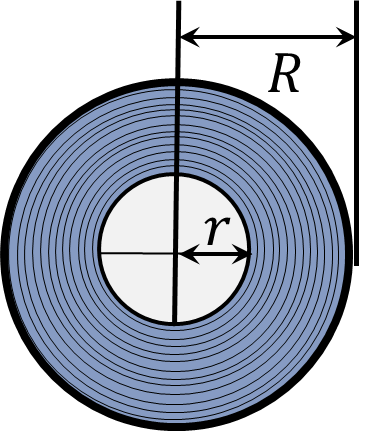
Пленка, намотанная на бобину, занимает площадь
$$S = \pi (R^2 - r^2)$$
Если пленка полностью разматывается со скоростью $v$ за время $t$, то длина пленки
$$l = vt$$
В поперечном сечении, пленка - это прямоугольник, площадь которого это $S$, а длина $l$. Тогда ширина этого прямоугольника(она же и толщина пленки)
$$\fbox{$d = \frac{S}{l} = \frac{\pi (R^2 - r^2)}{vt}$}$$