$1.5.6.$ Плоское твердое тело вращается вокруг оси, перпендикулярной его плоскости. Координаты начального положения точек $A$ и $B$ этого тела $(−1,\; 2)$ и $(3,\; 1)$, а конечного — $(−3,\;1)$ и $(−2,\; -3)$. Графическим построением найдите координаты оси вращения.
Т.к. ось вращения неподвижна, то все точки тела вращаются вокруг неё и перпендикулярны по направлению.
Если координаты двух точек в начале и в конце равны $A$, $B$ и $A'$, $B'$ соответственно, то если провести линии $AB$ и $A'B'$ точка их пересечения будет центром вращения
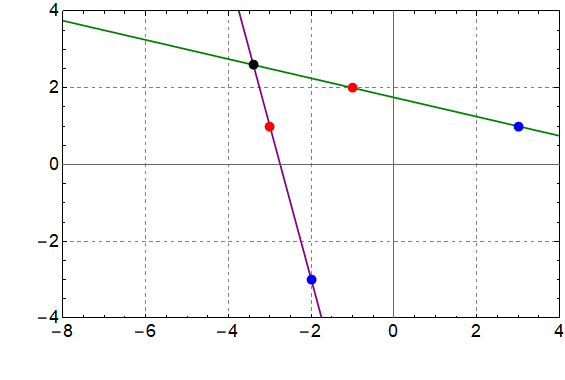
По построениям эта точка имеет координаты $(-3.4,\; 2.6)$