$1.5.8.$ Постройте траектории точек колеса, катящегося без проскальзывания по рельсу. Рассмотрите случаи, когда точки находятся от оси колеса на расстоянии: $r > R,\; r = R,\; r < R$. Найдите ускорение этих точек, если ось колеса движется с постоянной скоростью $v$. Найдите радиус кривизны траектории точки, находящейся в высшем и низшем положениях на расстоянии $r \neq R$ от оси колеса.
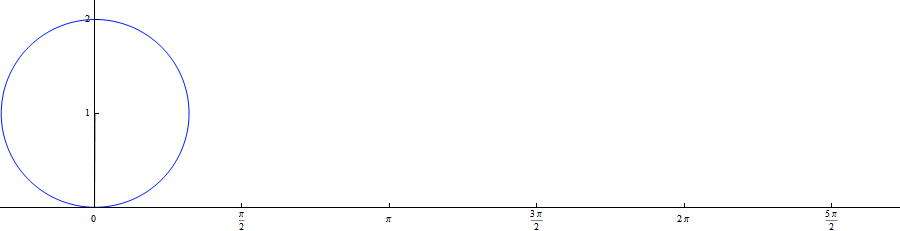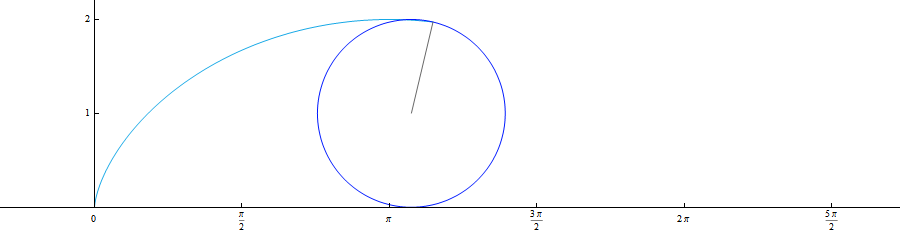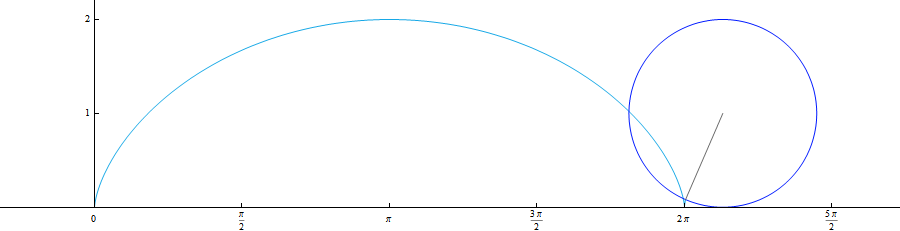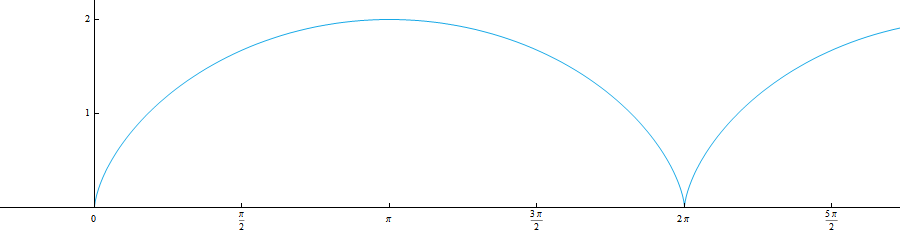
В данном случае, движение точек складывается из суммы поступательной скорости центра колеса и скорости вращения относительно этого центра, а ускорение точки высчитывается по обычной формуле центростремительного ускорения
$\fbox{$a = \omega^2 r = (v^2/R^2)r$}$
Для случая $r< R$, учитывая как вращательное так и поступательное движение, точка, расположенная на расстоянии $r$ в верхней точке своей траектории имеет скорость
$$u = \omega r + v = v(1 + \frac{r}{R})$$
Зная ускорение $a$ и скорость $u$ в данной точке, найдем ее радиус кривизны
$$r = \frac{u^2}{a}$$
$$\fbox{$r = \frac{(R+r)^2}{r}$}$$
Для большего понимания предлагаю иллюстрацию движения:
$a=(v^2/R^2)r; r_{в}=(R+r)^2/r, r_{н}=(R-r)^2/r.$