$1.5.9^*.$ Нить, намотанную на ось катушки, тянут со скоростью $v$ под углом $\alpha$ к горизонту. Катушка катится по горизонтальной плоскости без проскальзывания. Найдите скорость оси и угловую скорость вращения катушки. При каких углах $\alpha$ ось движется вправо? влево? Нить так длинна, что угол $\alpha$ не меняется при движении.
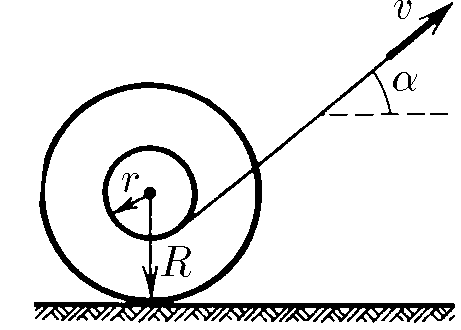
Радиус окружности, по которой катится катушка вокруг мгновенной оси, обозначим $ R^* $:
$ R^* = R \cos\alpha - r $
Угловая скорость катушки $ \omega$ определяется как отношение линейной скорости к радиусу:
$$ \omega = \frac{v}{R \cos\alpha - r} $$
Скорость оси $ v_0 $ можно найти, рассматривая вращение катушки как движение вокруг центра $ O $:
$ v_0 = \omega R $
Подставим найденную угловую скорость:
$$ v_0 = \frac{v R}{R \cos\alpha - r} $$
Катушка будет двигаться вправо, если скорость $ v_0 $ положительна, и влево, если $ v_0 $ отрицательна. Условие смены направления:
$ R \cos\alpha = r $
Соответственно, критический угол $ \alpha^* $ определяется из:
$$ \cos\alpha^* = \frac{r}{R} $$
$u=\frac{v R}{R \cos\alpha -r} ;$ $ \omega =\frac{v}{R \cos\alpha -r}$ вправо при $\cos\alpha >r / R$, влево при $\cos\alpha < r/R$