$11.1.14.$ а. Ускоритель плазмы (рельсотрон) состоит из двух параллельных массивных проводников (рельсов), лежащих в плоскости, перпендикулярной магнитному полю индукции $B$. Между точками $A$ и $C$ в водороде поджигают электрический разряд. Ток $I$ в разряде поддерживается постоянным. Под действием магнитного поля область разряда (плазменный сгусток) перемещается, разгоняясь к концам рельсов и срываясь с них. Чему равна скорость плазменного сгустка, если его масса $m$? Расстояние между рельсами $l$. Длина участка, на котором происходит ускорение плазмы, равна $L$.
б. Решите задачу для случая $B = 1 \,Тл$, $l = 0.1 \,м$, $L = 1 \,м$, $I = 10 \,А$; в плазменном сгустке содержится $10^{13}$ ионов водорода.
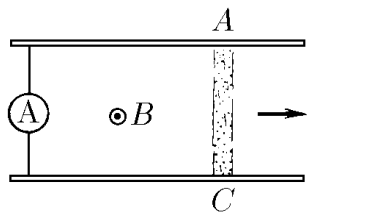
На промежутке длины $L$ на плазменный сгусток действует постоянная сила $$F_A = IBl$$ Тогда, из Закона Сохранения Энергии $$\frac{mv^2}{2} = F_AL$$ $$\frac{mv^2}{2} = IBlL$$ Откуда находим скорость $$\boxed{v=\sqrt{\frac{2BIlL}{m}}}$$
$$\mathrm{a.~}v=\sqrt{2BIlL/m}$$ $${6.~}v\approx1,1\cdot10^{7} \mathrm{~M/c.}$$