$11.1.22^*.$ В магнитном поле с большой высоты падает кольцо радиуса $a$ и массы $m$. Сопротивление кольца $R$. Плоскость кольца все время горизонтальна. Найдите установившуюся скорость падения кольца, если вертикальная составляющая индукции магнитного поля изменяется с высотой по закону $B = B_0(1+\alpha h)$.
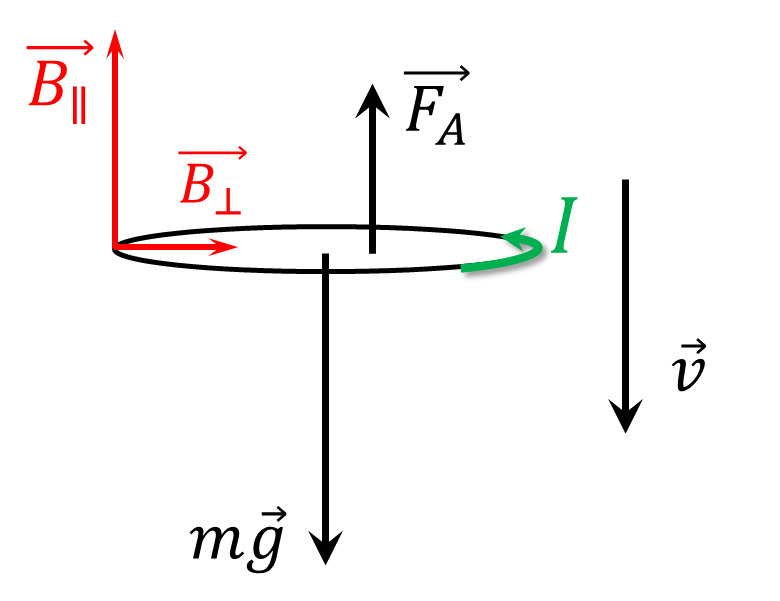
Кольцо будет лететь с потоянной скоростью, потому что сила Ампера $F_A$ будет компензировать силу тяжести $mg$
Через теорему о магнитном потоке, найдем тангенциальную составляющую магнитной индукции $$B_\parallel = - \frac{dB_\perp}{dh} \frac{a}{2}= - \frac{a}{2} \frac{d}{dh}(B_0(1+\alpha h)) $$ Учитывая, что установившаяся скорость постоянна $$v=\text{const}$$ $$\frac{dh}{dt} = -v$$ Откуда находим значение для тангенциальной составляющей магнитной индукции $B_\parallel$ $$B_\parallel = \frac{\alpha aB_0}{2}$$ Из-за того, что поток проходящий через кольцо изменяется, в кольце индуцируется ток $$\varepsilon_{i} = -\frac{d\Phi}{dt}=-\pi a^2 \frac{dB_\perp}{dt}$$ $$\varepsilon_{i} = \pi a^2 B_0v\alpha$$ По закону Ома, индуцированный ток найдём как $$I = \frac{\varepsilon_{i}}{R} = \frac{\pi a^2 B_0v\alpha}{R}$$ Тогда силу Ампера найдем как $$F_A = 2\pi aIB_\parallel$$ $$F_A = 2\pi a \frac{\pi a^2 B_0v\alpha}{R} \frac{\alpha aB_0}{2}$$ $$ F_A = \frac{\pi^2 a^4 B_0 ^2v \alpha^2}{R} $$ Условие отсутствия ускорения $$ mg = F_A$$ $$ \frac{\pi^2 a^4 B_0 ^2v \alpha^2}{R} = mg$$ Откуда получаем установившуюся скорость $$ \boxed{v = \frac{mgR}{(B_0\pi a^2\alpha )^2}}$$
NO: Более развернутую и красивую задачу с похожей идеей можно найти в "Очень длинных физических задачах" А.И.Слободянюка "Как гроб Магомета" (Задача 13)
$$ v = \frac{mgR}{(B_0\pi a^2\alpha )^2}$$