$11.1.25^*.$ Проводящий диск вращается с угловой скоростью $\omega$ в однородном магнитном поле индукции $B$, перпендикулярном плоскости диска. Что покажет амперметр, включенный через сопротивление $R$? Найдите ток, если $R = 1 \,Ом$, радиус диска $r = 0.05 \,м$, $\omega = 2\pi\cdot 50 \,рад/с$, $B = 1 \,Тл$.
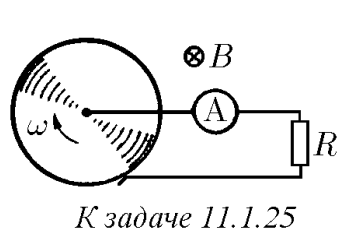
Вычислим ЭДС индукции между центром диска $О$ и скользящим контактом $А$, воспользовавшись определением ЭДС: ${E}_{i} = \frac{A_{ст}}{q}$ где $A_{ст}$ — работа сторонних сил (в данном случае это сила Лоренца) при перемещении положительного заряда из точки $А$ в точку $О$ Обозначим через $x$ — расстояние от заряда до центра $О$. Сила Лоренца, действующая на заряд: $F_{л} = qvB = q \omega xB ( \alpha = 90^{ \circ})$ Работа силы Лоренца: $A_{ст} = \int_{0}^{r} F_{л} dx $$= \int_{r}^{0} q \omega xB dx $$= q \omega B \int_{0}^{r} xdx $$= \frac{1}{2} q \omega r^{2} B$ может быть вычислена так же элементарно с помощью разбиения отрезка $АО$ на малые участки $\Delta x_{i} = x_{i+1} - x_{i}$ вычисления работы на каждом участке $A_{i} = q \omega B \frac{x_{i+1} + x_{i}}{2} (x_{i+1} - x_{i})$ и суммирования: $A_{} = \sum A_{i} $$= \sum q \omega B \frac{x_{i+1}^{2} - x_{i}^{2}}{2} = \frac{1}{2} q \omega B r^{2}$ Получаем, подставляя: $\varepsilon_{i}= \frac{1}{2} \omega Br^{2}$ Согласно закону Ома для полной цепи: $I = \frac{ \varepsilon_{i}}{R} = \frac{ \omega Br^{2}}{2R}$