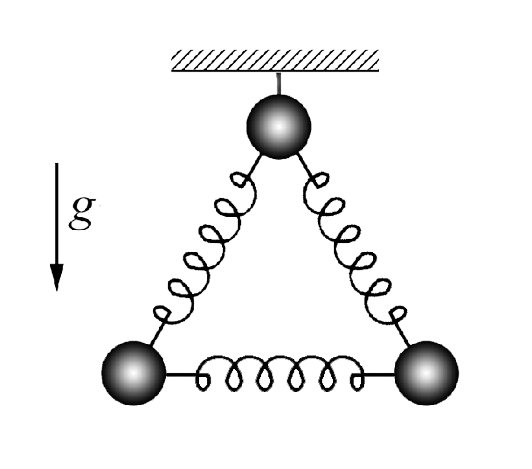
$2.1.13.$ Система из трех одинаковых шаров, связанных одинаковыми пружинами, подвешена на нити. Нить пережигают. Найдите ускорения шаров сразу после пережигания нити.
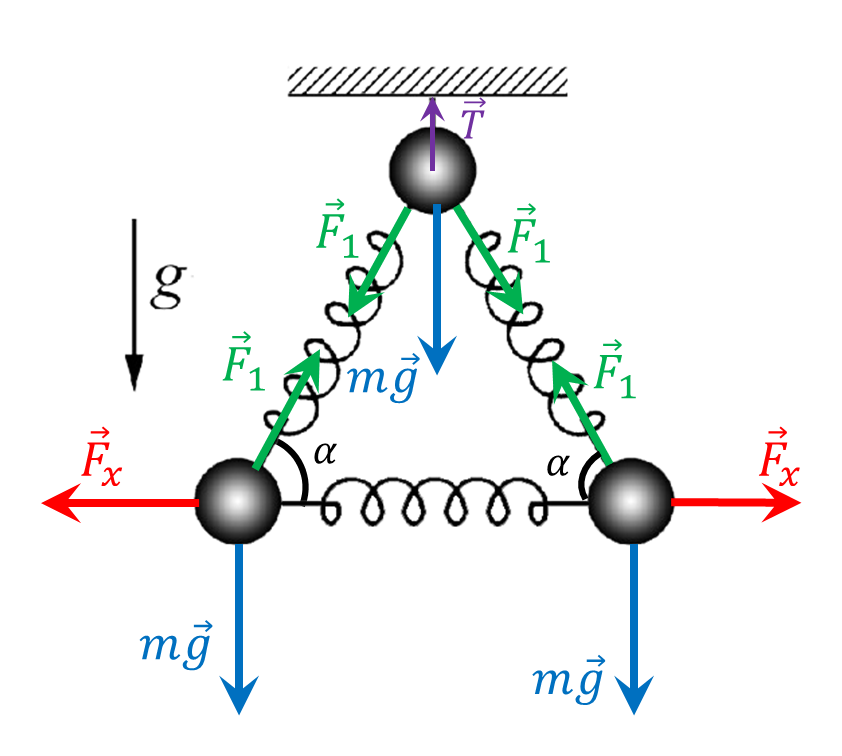
Запишем условие равновесия для двух нижных шаров на вертикальную и горизонтальную оси $$ \left\{\begin{matrix} mg = F_1 \sin\alpha\\ F_x = F_1 \cos\alpha& \end{matrix}\right.$$ где $P$ -сила давления маляра на кресло.
И для верхнего шарика $$T = mg + 2F_1 \sin\alpha$$ $$T = 3mg$$ Соответственно, когда нить перегорит, на верхний шарик будет вниз действовать сила $T=3mg$. Из второго закона Ньютона его начальное ускорение найдем как $$a = \frac{T}{m} = 3g$$ На нижние шарики, в горизонтальном направлении будут действовать сила $F_x$, которая будет компенсироваться силой $F_1 \cos\alpha$, а сила тяжести $mg$ — $F_1 \sin\alpha$
Таким образом, нижние шарики будут находиться в невесомости $$a=0$$ NO: Чем-то похожее явление происходит при падении "Слинки"

Советую интересную задачу про слинки IPhO 2019 "Springs and Slinky"
Ускорение верхнего шара равно $3g$, ускорение нижних — нулю.