$2.1.15.$ Тело массы $m$ соединено двумя пружинами жесткости $k_1$ и $k_2$ с неподвижными стенками, пружины первоначально не деформированы. При возникших колебаниях наибольшее ускорение тела равно $a$. Найдите максимальное отклонение тела от положения равновесия и максимальные силы, с которыми пружины действуют на стенки.
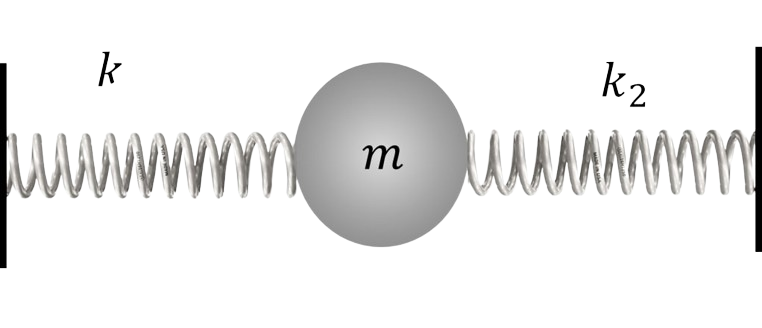
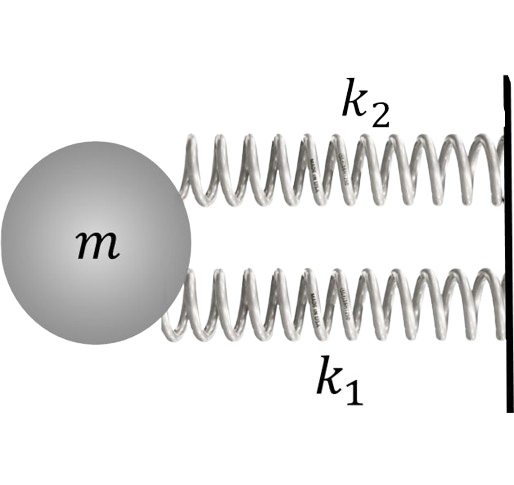
1. Пружины в данной задаче соединены параллельно, их деформация одинакова $$Δx_1 = Δx_2 = Δx$$ 2. Сила, действующая на массу со стороны пружин. определится в виде суммы $$F = F + F_1$$ , или $$k \Delta x = k_1 \Delta x + k_2 \Delta x$$ 3. Запишем уравнение движения массы под действием эквивалентной пру- жины жёсткостью ко, что позволит определить максимальное смещение $$ma = (k_1 + k_2) \Delta x_{max}$$ $$\Delta x_{max} = ma/(k_1 + k_2)$$ 4. Максимальные значения сил, действующих на массу $${F_1}_{max} = k_1 \Delta x_{max}$$ $${F_2}_{max} = k_2 \Delta x_{max}$$
$$x_{макс} = ma/(k_1 + k_2);$$ $${F_1}_{макс} = k_1x_{макс}$$ $${F_2}_{макс} = k_2x_{макс}$$