$2.1.17.$ Легкий магнит с крюком на вертикальной стальной плите остается неподвижным, пока подвешенный к нему груз не превосходит по массе $m_0$. Чему равна магнитная сила, если коэффициент трения магнита по стали равен $\mu$? С каким ускорением скользит магнитная подвеска, если масса груза $m > m_0$?
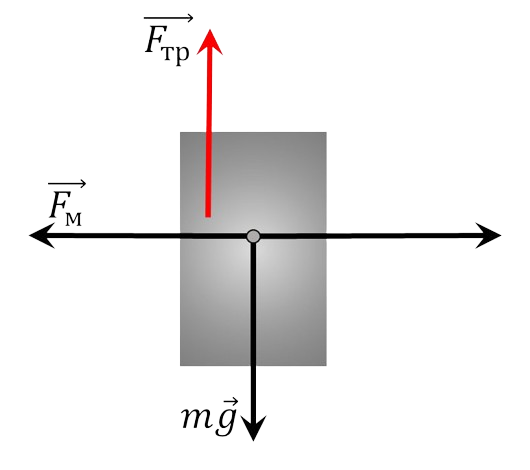
1. Тело можно рассматривать как свободное, если связи заменить их реакциями. Сила трения в данном случае вызывается действием магнитной силы, т.е. $$F_{тр} = \mu F_м$$ 2. Условие равновесия массы в этом случае будет иметь место при равенстве модулей силы тяжести и силы трения $$m_0 g = \mu F_м\Rightarrow \boxed{F_м = \frac{gm_0}{\mu}}$$ 3. Когда тело станет двигаться при $m > m_0$, то станет справедливо уравнение второго закона Ньютона, которое в проекции на ось $у$ запишется следующим образом $$mg - m_0 g = ma$$ $$\boxed{a = g \frac{m - m_0}{m}}$$
$$F = m_0g/\mu ;$$ $$a = g(m − m_0)/m$$