Условие:

$ 2.1.23.$ На тело массы $m$, лежащее на горизонтальной плоскости, действует сила $F$ под углом $\alpha$ к горизонту. Коэффициент трения $\mu$. Найдите ускорение тела, если оно не отрывается от плоскости.

Решение:

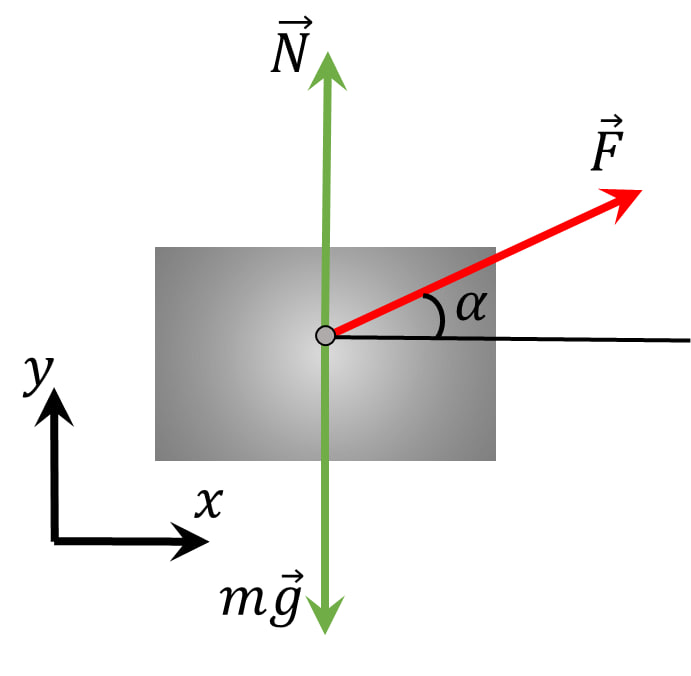
1. Нормальная реакция связи в данном случае будет определяться как силой тяжести $mg$, так и проекцией на ось $OY$ приложенной силы:

$N=mg-F \, \sin\alpha$

Сила трения определится как:

$F_{тр} = (mg-F \,\sin\alpha )$

2. Основной закон динамики, таким образом. запишется следующим образом:

$F \, \cos\alpha = \mu (mg-F \,\sin\alpha )$

3. Из уравнения второго закона Ньютона легко определить искомое ускорение

$a = \frac{1}{m}(F\cos\alpha -\mu mg+F\,\sin\alpha )$

$a = \frac{F}{m}(\cos\alpha -\mu\,\sin\alpha )$

Ответ: $a = (F/m)(\cos\alpha + \mu\,\sin\varphi)$$ − \mu g$, если это выражение больше нуля, иначе $a = 0$.