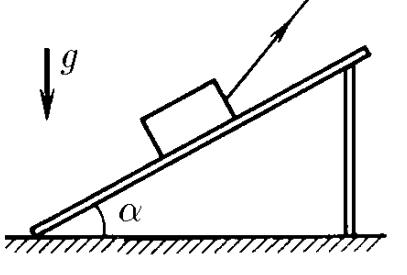
$2.1.26^*.$ По деревянным сходням, образующим угол $\alpha$ с горизонтом, втаскивают за привязанную к нему веревку ящик. Коэффициент трения ящика о сходни $\mu$. Под каким углом к горизонту следует тянуть веревку, чтобы с наименьшим усилием втащить ящик?
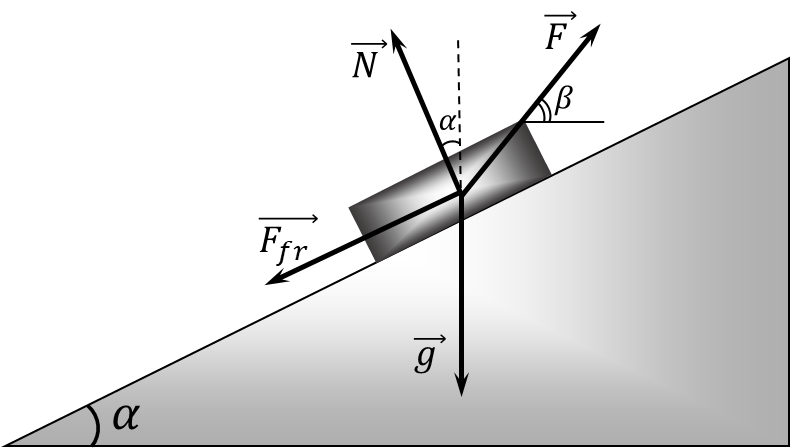
Рассмотрим силы, действующие на ящик (рис.). Это - сила тяжести $ m \vec{g} $, сила натяжения веревки $ \vec{F} $, сила реакции соударения $ \vec{N} $ и сила трения $ \vec{F}_{тр} $, величина которой $ \vec{F}_{тр} = \mu N $. Спроктируем все силы на направление вдоль схождения и перпендикулярно к ним и запишем соответственные уравнения движения.
Так как ящик не перемещается в направлении, перпендикулярном схождению, то сумма проекций сил на это направление должна быть равна нулю, то есть
\[ N + F \sin ( \beta - \alpha ) - mg \cos\alpha = 0, \tag{1} \]
Вдоль схождения ящик движется с ускорением $ a $ (в частном случае при равномерном движении $ a = 0 $), поэтому сумма проекций сил должна быть равна $ ma $:
\[ F \cos( \beta - \alpha ) - mg \sin\alpha - \mu N = ma. \tag{2} \]
Из уравнений (1) и (2) получаем:
\[ F = \frac{ma + mg ( \sin\alpha + \mu\cos\alpha )}{ \cos ( \beta - \alpha ) + \mu\sin ( \beta - \alpha ) }. \tag{3} \]
В полученное выражение для силы $ F $ угол $ \beta$ входит только знаменатель. Следовательно, величина силы $ F $ будет минимальной при таком значении угла $ \beta$, при котором знаменатель в формуле (3) максимален, то есть максимальна величина
\[ \cos ( \beta - \alpha ) + \mu\sin ( \beta - \alpha ). \]
Сделаем некоторые преобразования. Представим коэффициент трения $ \mu$ как тангенс некоторого угла $ \gamma$:
\[ \tan\gamma = \mu ; \quad \gamma = \arctan \mu ; \] \[ \sin\gamma = \frac{ \mu}{ \sqrt{1 + \mu^{2} } }; \quad \cos\gamma = \frac{1}{ \sqrt{1 + \mu^{2} } }. \]
Тогда можно записать:
\[ \cos ( \beta - \alpha ) + \mu\sin ( \beta - \alpha ) = \sqrt{1 + \mu^{2} } \cos ( \beta - \alpha - \gamma ). \]
Последнее выражение максимально и равно
\[ \sqrt{1 + \mu^{2}} \quad \text{при} \quad \beta - \alpha - \gamma = 0, \quad \text{то есть при} \quad \beta = \alpha + \gamma = \alpha + \arctan \mu . \tag{4} \]
При таком значении угла $ \beta$ и минимальна сила $ F $. Причем, если ящик движется равномерно ($ a = 0 $), то
\[ F_{min} = \frac{mg( \sin\alpha + \mu\cos\alpha ) }{ \sqrt{1 + \mu^{2} } }. \]
а при движении с ускорением $ a $
\[ F_{min} = \frac{ma + mg ( \sin\alpha + \mu\cos\alpha ) }{ \sqrt{1 + \mu^{2} } }. \]
Однако, это решение верно не для любого ускорения. Так как направление силы $ \vec{F} $ не зависит от $a$, а абсолютная величина силы $ \vec{F} $ увеличивается с увеличением ускорения, то при некотором значении ускорения $ a = a_0 $ сила $ \vec{F} $ станет такой, что ее составляющая $ F \sin (\beta - \alpha ) $, перпендикулярная к наклонной плоскости, будет равна по абсолютной величине составляющей силы тяжести $ mg \cos\alpha$. При этом обратится в нуль как сила $ \vec{N} $, так и сила $ \vec{F}_{тр} $. В дальнейшем (при $ a > a_0 $) для того чтобы ящик не оторвался от полозьев, направление силы $ \vec{F} $ должно меняться с увеличением ускорения так, чтобы составляющая силы $ \vec{F} $, перпендикулярная к наклонной плоскости, оставалась равной составляющей силы тяжести, то есть \[ F \sin (\beta - \alpha ) = mg \cos\alpha\] Для составляющих этих сил, параллельных наклонной плоскости, можно записать \[ F \cos (\beta - \alpha ) - mg \sin\alpha = ma \] Из двух последних равенств найдем \[ \tan (\beta - \alpha ) = \frac{g \cos\alpha}{g \sin\alpha + a} \] откуда \[ \beta = \alpha + \arctan \frac{g \cos\alpha}{g \sin\alpha + a} \] Величину $ a_0 $ можно найти из тех соображений, что при $ a = a_0 $ значение угла $ \beta$ из (4) и (5) совпадают: \[ \alpha + \arctan \frac{g \cos\alpha}{g \sin\alpha + a_0 } = \alpha + \arctan \mu\] откуда \[ a_0 = g \left( \frac{\cos\alpha}{\mu} - \sin\alpha\right) \] Итак, при $ a \leq a_0 $ (следовательно, и при равномерном движении тоже) \[ \beta = \alpha + \arctan \mu\] При $ a > a_0 $ \[ \beta = \alpha + \arctan \frac{g \cos\alpha}{g \sin\alpha + a} \] Мы решили задачу. Однако, приведем еще одно решение. Это - красивое геометрическое решение. При равномерном движении вдоль склонней сумма всех сил должна быть равна нулю. Заменим силы $ \vec{N} $ и $ \vec{F}_{тр} $ их равнодействующей $ \vec{Q} = \vec{N} + \vec{F}_{тр} $ (рис.) и будем складывать силы $ \vec{Q}, \vec{F} $ и $ m \vec{g} $. Они должны образовать замкнутый треугольник. Заменим, что направление силы $ \vec{Q} $ составляет с перпендикуляром к наклонной плоскости угол $ \delta$ такой, что \[ \tan\delta = \frac{F_{тр}}{N} = \frac{\mu N}{N} = \mu\]
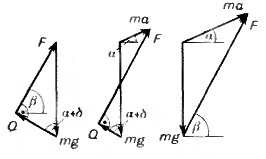
Таким образом, при изменении величины и направления силы $ \vec{F} $ направление силы $ \vec{Q} $ остается неизменным. Следовательно, абсолютная величина силы $ \vec{F} $ будет минимальна, если он перпендикулярен к вектору $ \vec{Q} $ (рис.). (так как величина и направление вектора $ m \vec{g} $ неизменны), то минимальная сила будет равна: \[ F_{\min} = mg \sin\alpha + mg \mu\cos\alpha = mg (\sin\alpha + \mu\cos\alpha ) \] Таким образом, величина минимальной силы, необходимой для подъема ящика с ускорением $ a \leq a_0 $ равна \[ F_{\min} = mg (\sin\alpha + \mu\cos\alpha ) \] Если ускорение $ a > a_0 $, то для минимальной силы $ \vec{F} $, направленной под углом $ \beta$ к горизонтали, имеем: \[ \beta = \alpha + \arctan \frac{g \cos\alpha}{g \sin\alpha + a} \]
$$\beta = \alpha + \arctan \mu$$