$2.1.28.$ На обледеневшем участке шоссе коэффициент трения между колесами и дорогой в десять раз меньше, чем на необледеневшем. Во сколько раз нужно уменьшить скорость автомобиля, чтобы тормозной путь на обледеневшем участке шоссе остался прежним?
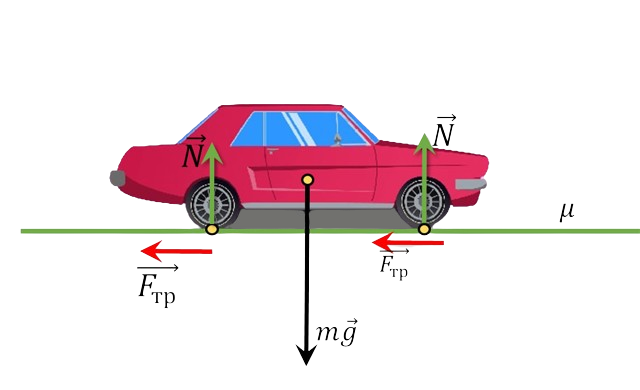
1. Внешней силой при движении автомобиля является сила трения $F = \mu mg$, поэтому без учёта сопротивления со стороны воздуха, динамическое уравнение движения имеет вид $$ma = \mu mg$$ $$a = \mu g$$ 2. Кинематические уравнения движения в данном случае представятся следующим образом $$\left\{\begin{matrix} v = v_0-at \\ x=v_0-\frac{at^2}{2} \end{matrix}\right.$$ $$t=\frac{v_0}{a}=\frac{v_0}{\mu g}$$ 3. При подстановке во второе уравнение системы значений ускорения и времени, получим уравнение тормозного пути автомобиля $$x=\frac{v_0^2}{\mu g}-\frac{v_0^2}{2\mu g}=\frac{v_0^2}{2\mu g}$$ $$v_0 = \sqrt{2\mu gx}$$ Отсюда скорость нужно уменьшить в $\sqrt{10}$ раз