$2.1.29.$ Автомобиль с мощным двигателем, трогаясь с места, за $5 \,с$ набирает скорость $72 \,км/ч$. Найдите коэффициент трения между колесами и дорогой. Каков наименьший тормозной путь автомобиля, набравшего эту скорость?
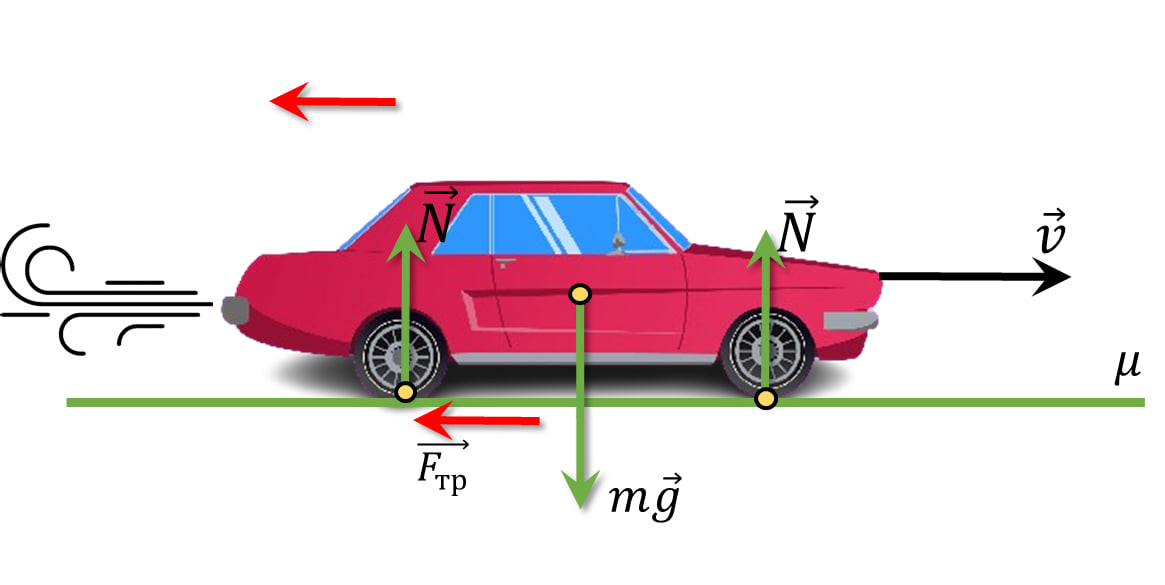
Находим величину замедления $$a = -\frac{\Delta v}{\Delta t} = -4 \,\frac{м}{с}$$ $$\Delta t = \frac{\Delta v}{a}$$ 2. Кинематические уравнения движения в данном случае представятся следующим образом $$\boxed{x=v_0t-\frac{v \Delta t^2}{2}=\frac{v_0^2}{2a}=50 \,м}$$ Найдем Коэфицент трения $\mu$: $$ma = \mu mg$$ $$\boxed{\mu = \frac{a}{g} = 0.4}$$
$$\mu\approx 0.4\text{; }l \approx 50 \text{ м}$$