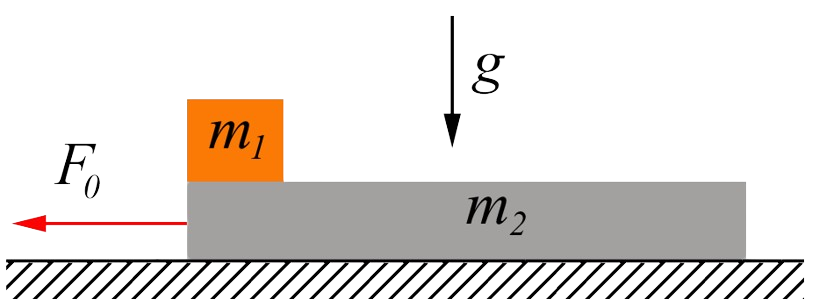
$2.1.30^*.$ Тело массы $m_1$ лежит на доске массы $m_2$, находящейся на гладкой горизонтальной плоскости. Коэффициент трения между телом и доской $\mu$.
а. Какую силу надо приложить к доске, чтобы тело соскользнуло с нее? За какое время тело соскользнет, если к доске приложена сила $F_0$, а длина доски равна $l$?
б. С каким ускорением движутся тело и доска, если сила $F_0$ действует на тело массы $m_1$?
$а)$ Чтобы тело начало скольжение прикладываемая сила должна превосходить силу трения. При определении величины силы трения необходимо учесть, что в соответствии с третьим законом Ньютона тело действует на доску, а доска на тело, поэтому будет проявляться двойная сила трения $$F_t = \mu g (m_1 + m_2)$$ Условие начала движения: $$\boxed{F > \mu g (m_1 + m_2)}$$ Для определения времени скольжения воспользуемся кинематическими уравнениями: $$l = \frac{a t^2}{2} \Rightarrow t = \sqrt{\frac{2L}{a}}$$ Ускорение a при действии вдоль доски постоянной силы $F_0$, определим из уравнения второго закона Ньютона в проекции на направление движения: $$F_0 - F_t = m_1 a$$ $$a = \frac{F_0 - \mu g (m_1 + m_2)}{m_1}$$ Время скольжения: $$\boxed{t = \sqrt{\frac{2 L m_1}{F_0 - \mu g (m_1 + m_2)}}}$$
$б)$ На тело действует две внешние силы $F_0$ и сила трения $F_{тр}$. Запишем второй закон Ньютона для тела $$m_1a_1 = F_0 - F_{тр}$$ Учитывая, что $$F_{тр} = \mu N = \mu m_1 g$$ $$m_1a_1 = F_0 - \mu m_1 g$$ Откуда $a_1$ найдём как $$\boxed{a_1 = \frac{F_0 - \mu m_1 g}{m_1}}$$ Между тем, из внешних сил на доску действует только сила трения с бруском
Тогда второй закон Ньютона для доски $$m_2a_2 = \mu m_1 g$$ Выражаем $a_2$ $$\boxed{a_{2}=\mu g\frac{m_{1}}{m_{2}}}$$
$$\text{a.} F>\mu (m_{2}+m_{1})g\text{, }t=\sqrt{\frac{2lm_{2}}{F_{0}-\mu (m_{2}+m_{1})g}}$$ $$\text{б.} a_{1}=\frac{F_{0}-\mu m_{1}g}{m_{1}}\text{, }a_{2}=\mu g\frac{m_{1}}{m_{2}}.$$