$2.1.41.$ Какая шайба, вращающаяся вокруг своей оси или не вращающаяся, пройдет больший путь до остановки на шероховатой горизонтальной поверхности? Начальная скорость центров шайб одинакова.
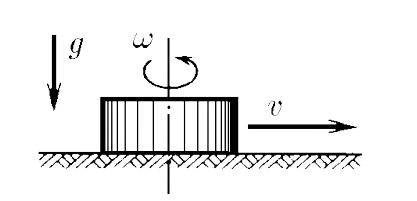
1. Поступательно движущаяся шайба обладает только кинетической энергией поступательного движения $$K_1=\frac{mv^2}{2}$$ плоское движение шайбы, представляющее собой суперпозицию поступательного и вращательного движений, характеризуется двумя составляющими кинетической энергии: поступательной и вращательной: $$K_2=\frac{mv^2}{2}+J_z\frac{\omega^2}{2}$$ $$K_2=\frac{mv^2}{2}+\frac{mr^2}{2}\cdot\frac{\omega^2}{2}$$ $$K_2=\frac{m}{2}(v^2+\frac{r^2 \omega^2}{2})$$ $$K_2=\frac{3}{4}mv^2$$ $$K_2>K_1$$ 2. Начальная кинетическая энергия шайб в обоих случаях будет расходоваться на работу против силы трения $$A_{тр} = \mu mg\Delta x$$ 3. В соответствии с теоремой об изменении кинетической энергии: $$\frac{K_2}{K_1}=\frac{\Delta x_2}{\Delta x_1}=1.5$$