$2.1.45^*.$ На плоскости, тангенс угла наклона которой равен коэффициенту трения, лежит монета. В горизонтальном направлении вдоль плоскости монете сообщили скорость $v$. Найдите установившуюся скорость монеты.
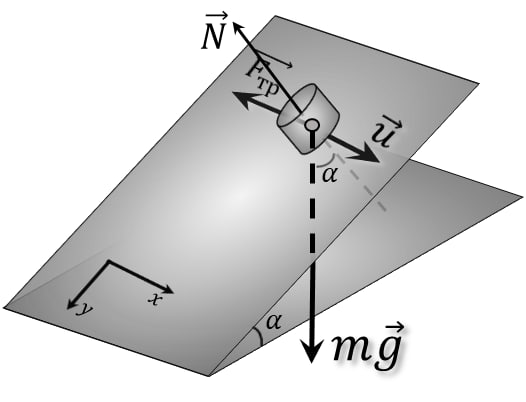
Проектируем $m\vec{g}$ на $OY$:
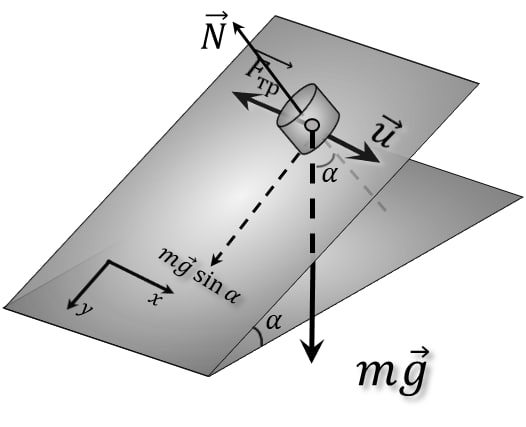
Из рисунка, найдем силу реакции опоры: $$N=mg \cos\alpha$$ По Закону Амонтона — Кулона: $$F_{тр}=\mu N=\mu mg \cos\alpha$$ Т.к. $\mu = \tan\alpha$ (по условию): $$F_{тр}=\mu mg \cos\alpha$$ $$F_{тр}=mg \cdot \tan\alpha\cdot \cos\alpha =mg \sin\alpha$$ $$F=mg \sin\alpha$$ Перерисуем в плоскости $XY$ В начальный момент $(\varphi=90^{\circ})$:
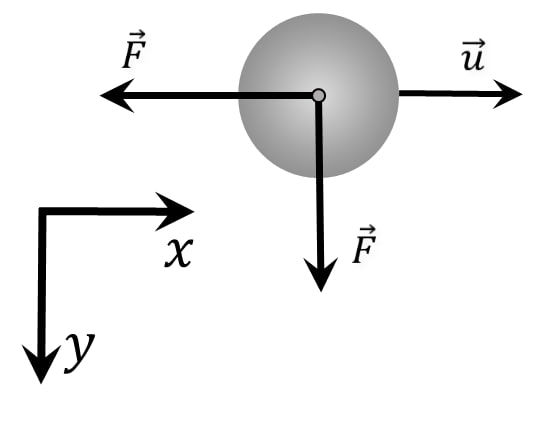
В конечный момент $(\varphi=0^{\circ})$:
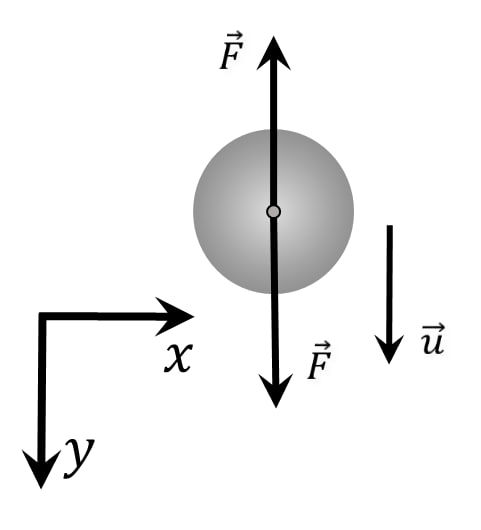
Рассмотрим, произвольный момент:
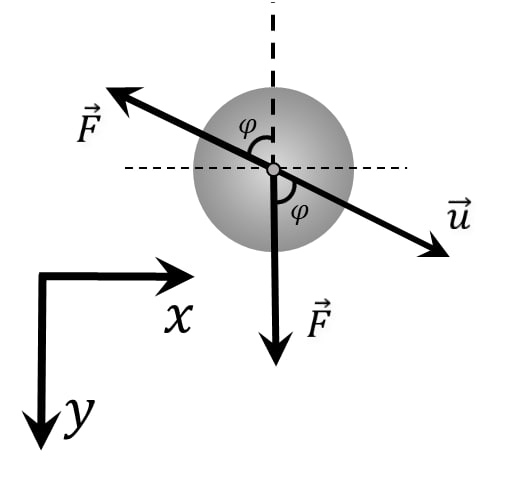
Заметим, что $\varphi$ меняется от $0^{\circ}$ до $90^{\circ}$:
Запишем второй закон Ньютона: $$\left\{\begin{matrix} \frac{du_x}{dt} = \frac{F \sin \varphi }{m}& \\ \frac{du_y}{dt} = \frac{F (1- \cos \varphi) }{m} & \end{matrix}\right.$$ $$\left\{\begin{matrix} \frac{d}{dt} (u \sin\varphi)= \frac{F \sin \varphi }{m}& \\ \frac{d}{dt} (u \cos\varphi) = \frac{F (1- \cos \varphi) }{m} & \end{matrix}\right.$$ Решаем систему дифференциальных уравнений: $$\left\{\begin{matrix} \frac{d\varphi}{dt} = \frac{F \sin \varphi }{mu}& (a)\\ \frac{du}{dt} = \frac{F (1- \cos \varphi) }{m} & (b) \end{matrix}\right.$$ Разделим $(b)$ на $(a)$: $$\frac{du}{d\varphi} = u\frac{1- \cos \varphi}{\sin \varphi}$$ $$\frac{du}{u} = \frac{1- \cos \varphi}{\sin \varphi} d\varphi$$ $$\frac{du}{u} = tg (\frac{\varphi}{2}) d\varphi$$ Интегрируем обе части уравнения: $$\int \frac{du}{u} = \int tg (\frac{\varphi}{2}) d\varphi \; (c)$$ $$\int\frac{du}{u}=ln|u| \; (d)$$ $$\int tg (\frac{\varphi}{2}) d\varphi=-2 ln(\cos(\frac{x}{2})) \; (e)$$ Подставляем $(e)$ и $(d)$ в $(c)$:
$$ln(v)+C=ln(\sin(\varphi)) -(ln(\sin(\frac{\varphi}{2})-\cos(\frac{\varphi}{2})))\; (e)$$
$$v_x=\frac{v}{2}$$
$$\frac{v}{2}$$