$2.1.47^*.$ Найдите ускорение тел системы, изображенной на рисунке. Сила $F$ приложена по направлению нити к одному из тел массы $m$. Участки нити по обе стороны от легкого блока, прикрепленного к телу массы $M$, параллельны
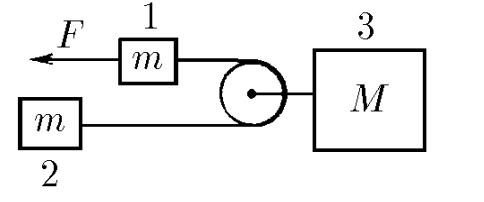
Тело массой $m_3$ движется с ускорения центра масс системы
Рассматривая систему целиком(не учитывая внутренних сил) $$\boxed{a_3 = \frac{F}{M+2m}}$$ При этом на тело $m_3$ действует сила, эквивалентная двойной силе натяжения нити $2T$ $$2T = M a_3$$ $$T = F\frac{M}{2(M+2m)}$$ На тело $m_1$ действует две силы $\vec{T}$ и $\vec{F}$
Второй закон Ньютона для первого тела запишем как $$F-T = ma_1$$ $$\boxed{a_1=\frac{F(M+4m)}{2m(M+2m)}}$$ Аналогично, на второе тело $m_2$ действует только $\vec{T}$ $$m_2 = T$$ $$\boxed{a_2=\frac{FM}{2m(M+2m)}}$$
Ускорения грузов 1–3: $$a_1=\frac{F(M+4m)}{2m(M+2m)}$$ $$a_2=\frac{FM}{2m(M+2m)}$$ $$a_3=\frac{F}{M+2m}$$