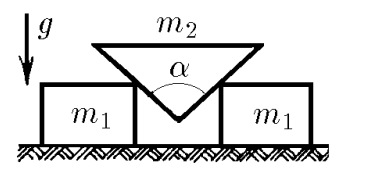
$2.1.48.$ Между двумя одинаковыми гладкими брусками массы $m_1$ каждый вставлен клин массы $m_2$ с углом $\alpha$. Определите ускорение тел.
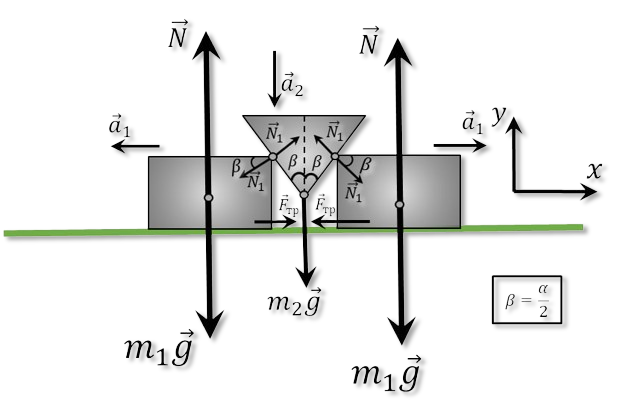
Рассмотрим малое смещение за время $dt$ с точки зрения кинематики:
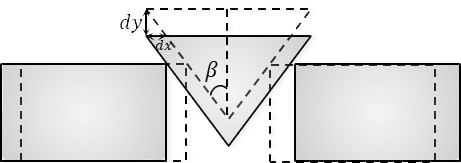
Из геометрических соображений: $$dy = dx \cdot c\tan\beta$$ Продеффиринцируем дважды обе части выражения: $$\frac{dy}{d^2t} = \frac{dx}{d^2t} \cdot c\tan\beta$$ $$a_1 = a_2 \cdot \tan\beta\quad(1)$$ Т.к. Автор не сказал ничего про трение, пример $F_{тр}=0$ Далее, запишем 2 закон Ньютона для бруска $m_1$ на ось $OY$: $$m_1a_1=N_1\cos\beta$$ $$N_1=\frac{m_1a_1}{\cos\beta}\quad(a)$$ Аналогично для $m_2$: $$m_2a_2=m_2g-2N_1\,\sin\beta\quad(b)$$ Подставляем $(a)$ в $(b)$: $$m_2a_2=m_2g-2m_1a_1\cdot \tan\beta$$ Подставляем $(1)$ в $(c)$: $$m_2a_2=m_2g-2m_1a_2\cdot \tan^2\beta$$ Выражаем $a_2$: $$\boxed{a_2=\frac{m_2g}{m_2+2m_1\,\tan^2\beta}}\quad(d)$$ Учитывая $(1)$, домнажаем $(d)$ на $\tan\beta$: $$\boxed{a_1=\frac{m_2g\,\tan\beta}{m_2+2m_1\,\tan^2\beta}}$$
$$a_1=\frac{m_2g\,\tan\beta}{m_2+2m_1\,\tan^2\beta}$$ $$a_2=\frac{m_2g}{m_2+2m_1\,\tan^2\beta}$$
Попробуйте объяснить парадокс:
Опишем движение центра масс системы на ось $OY$:
$$(2m_1+m_2)a_y=2m_1\vec{g}+m_2\vec{g}+2\vec{N}+2\vec{N_1}-2\vec{N_1}+\vec{F_{тр}}-\vec{F_{тр}}$$
Т.к. $\vec{N_1}$ и $\vec{F_{тр}}$ — внутренние силы и компенсируют друг друга, a $\vec{N}$ компенсируют $m_1\vec{g}$ $$(2m_1+m_2)a_y=m_2g$$ $$a_y=g\frac{m_2}{2m_1+m_2}$$ Т.к. грузы массой $m_1$ лежат на поверхности $(y=const)$ $$a_2=a_y=g\frac{m_2}{2m_1+m_2}\quad(2)$$ Подставляем $(2)$ в $(1)$: $$a_1 = a_2 \cdot \tan\beta$$ $$a_2=g\frac{m_2 \,\tan\beta}{2m_1+m_2}$$ Что не является ответом!