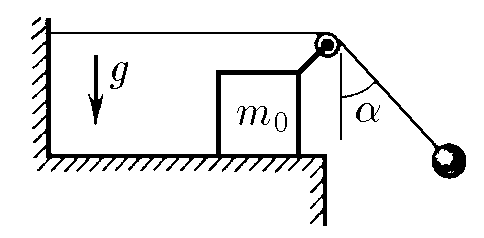
$2.1.49^*.$ К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен груз. Ролик закреплен на бруске массы $m_0$, который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют от вертикали на угол $\alpha$ и затем отпускают. Определите ускорение бруска, если угол, образованный нитью с вертикалью, не меняется при движении системы. Чему равна масса груза?
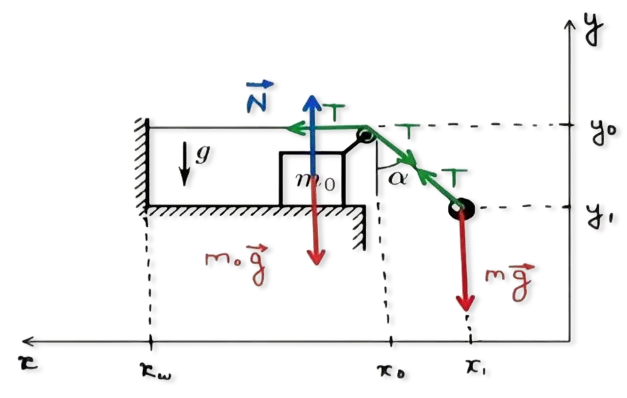
Применим второй закон Ньютона: $$OX: \;T - T \sin\alpha = m_0 a_{0x} $$ $$ T \sin\alpha = m_{a1x} $$ $$OY: \;N - mg - T \cos\alpha = m_0 a_{0y} = 0 $$ $$ T \cos\alpha - mg = m_{a1y} $$ $$ \tan\alpha = \frac{x_0 - x_1}{y_0 - y_1} $$ Учитывая $\alpha = \text{const}$
$$ \frac{d}{dt} \left( \tan\alpha\right) = \frac{\left( \frac{dx_0}{dt} - \frac{dx_1}{dt} \right)(y_0 - y_1) - \left( \frac{dy_0}{dt} - \frac{dy_1}{dt} \right)(x_0 - x_1)}{(y_0 - y_1)^2} = 0 $$
$$ \frac{d}{dt} \left( \left( \frac{dx_0}{dt} - \frac{dx_1}{dt} \right)(y_0 - y_1) \right) = \frac{d}{dt} \left( \left( \frac{dy_0}{dt} - \frac{dy_1}{dt} \right)(x_0 - x_1) \right) $$
$$ \left(\frac{d^{2}x_{0}}{dt^{2}}-\frac{d^{2}x_{1}}{dt^{2}}\right)(y_{0}-y_{1})+\left(\frac{dx_{0}}{dt}-\frac{dx_{1}}{dt}\right)\left(\frac{dy_{0}}{dt}-\frac{dy_{1}}{dt}\right)=$$ $$\left(\frac{d^{2}y_{0}}{dt^{2}}-\frac{d^{2}y_{1}}{dt^{2}}\right)(x_{0}-x_{1})+\left(\frac{dy_{0}}{dt}-\frac{dy_{1}}{dt}\right)\cdot\left(\frac{dx_{0}}{dt}-\frac{dx_{1}}{dt}\right) $$
$$ (a_{0x} - a_{1x})(y_0 - y_1) = (a_{0y} - a_{1y})(x_0 - x_1) $$ $$ \tan\alpha (a_{0y} - a_{1y}) = a_{0x} - a_{1x}$$ Из (1) $$a_{0y} = 0$$ $$ -\tan\alpha\, a_{1y} = a_{0x} - a_{1x} $$ Длина веревки: $$ L = x_w - x_0 + \frac{y_0 - y_1}{\cos\alpha} $$ Т.к. нить нерастяжима
$$ \frac{d^2 L}{dt^2} = -\frac{d^2 x_0}{dt^2} + \frac{1}{\cos\alpha} \left( \frac{d^2 y_0}{dt^2} - \frac{d^2 y_1}{dt^2} \right) = 0 $$
$$ \left( \frac{d^2 x_0}{dt^2} = a_{0x}, \frac{d^2 y_0}{dt^2} = a_{0y}, \frac{d^2 y_1}{dt^2} = a_{1y} \right) $$
$$ a_{0x} \cdot \cos\alpha = a_{0y} - a_{1y}$$ Из $(1)$: $a_{0y} = 0$ $$ a_{0x} \cos\alpha = -a_{1y} $$ Разделив уравнения из (1):
$$ \frac{T \sin\alpha}{T \cos\alpha} = \frac{m a_{1x}}{m (g + a_{1y})} \to \tan\alpha (g + a_{1y}) = a_{1x} $$
$$ \tan\alpha a_{1y} = a_{1x} - g \tan\alpha$$ и используя (4) $$\boxed{a_{0x} = g \tan\alpha}$$ Разделив уравнения из (1): $$ \frac{T(1 - \sin\alpha )}{T \cos\alpha} = \frac{M}{m} \cdot \frac{a_{0x}}{g + a_{1y}}$$ Обратите внимание, что: $$a_{1y} = -g \sin\alpha$$ $$ \frac{1 - \sin\alpha}{\cos\alpha} \frac{M}{m} = \frac{g \tan\alpha}{g - g \sin\alpha} \to m = \frac{M \sin\alpha}{(1 - \sin\alpha )^2} $$ $$ \boxed{m = \frac{M \sin\alpha}{(1 - \sin\alpha )^2}} $$
$$a = g \tan\alpha$$ $$m = m_0 \frac{\sin\alpha}{(1 − \sin\alpha )^2}$$