$2.1.5.$ Какая сила действует в поперечном сечении однородного стержня длины $l$ на расстоянии $x$ от того конца, к которому вдоль стержня приложена сила $F$?
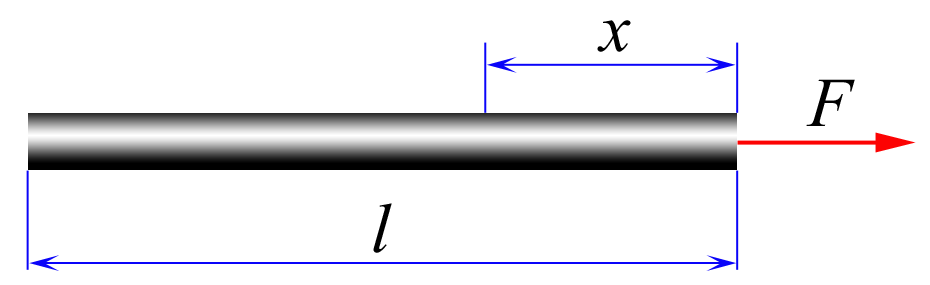
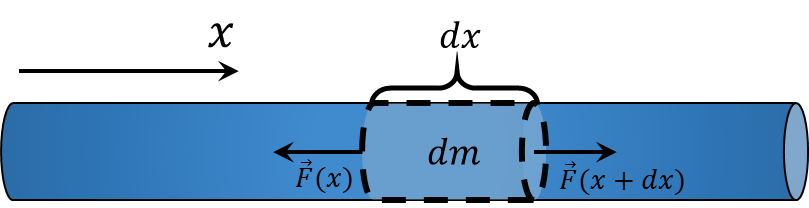
Если рассматривать стержень массой $m$ как единое целое, то он будет двигаться с ускорением $$a = \frac{F}{m}$$ Т.к. стержень нерасстяжим, то ускорение всех его частей одинаково и равно $a$
Рассмотрим малый участок стержня длины $dx$ и массы $dm$. Т.к. стержень однородный $$dm = m \frac{dx}{l}$$ Запишем второй закон ньютона для этого участка. $$a\, dm = F(x+dx) - F(x)\quad(1)$$ Где $F(x+dx)$ и $F(x)$ сила взаимодействия вместе с соседями
Проинтегрируем выражение $(1)$ по горизонтальной координате $x$: $$\int_x^l am\frac{dx}{l} = \int_x^l dF$$ $$ma\frac{l-x}{l} $$ $$F(x) = \fbox{$F(1-\frac{x}{l})$}$$
$$\fbox{$T = F(1 − x/l)$}$$