Условие:

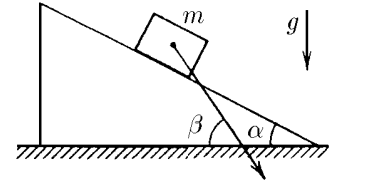
$2.1.50.$ На гладкой горизонтальной плоскости находится клин с углом $\alpha$ при основании. Тело массы $m$, положенное на клин, опускается с ускорением, направленным под углом $\beta > \alpha$ к горизонтали. Определите массу клина.

Решение:

Силы действующие на систему

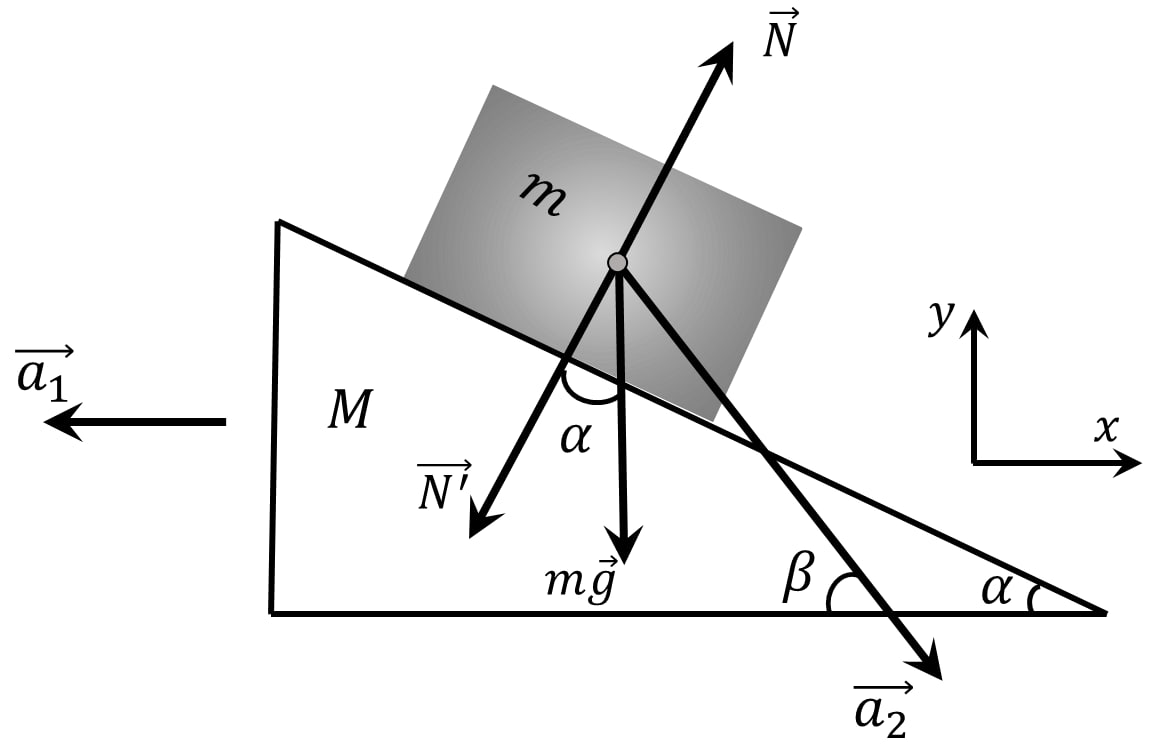
Разобьём ускорение бруска $\vec{a}_2$ на нормальную $\vec{a}_n$ и тангенциальную $\vec{a}_\tau$ компоненты

Нормальное и тангенциальное ускорения

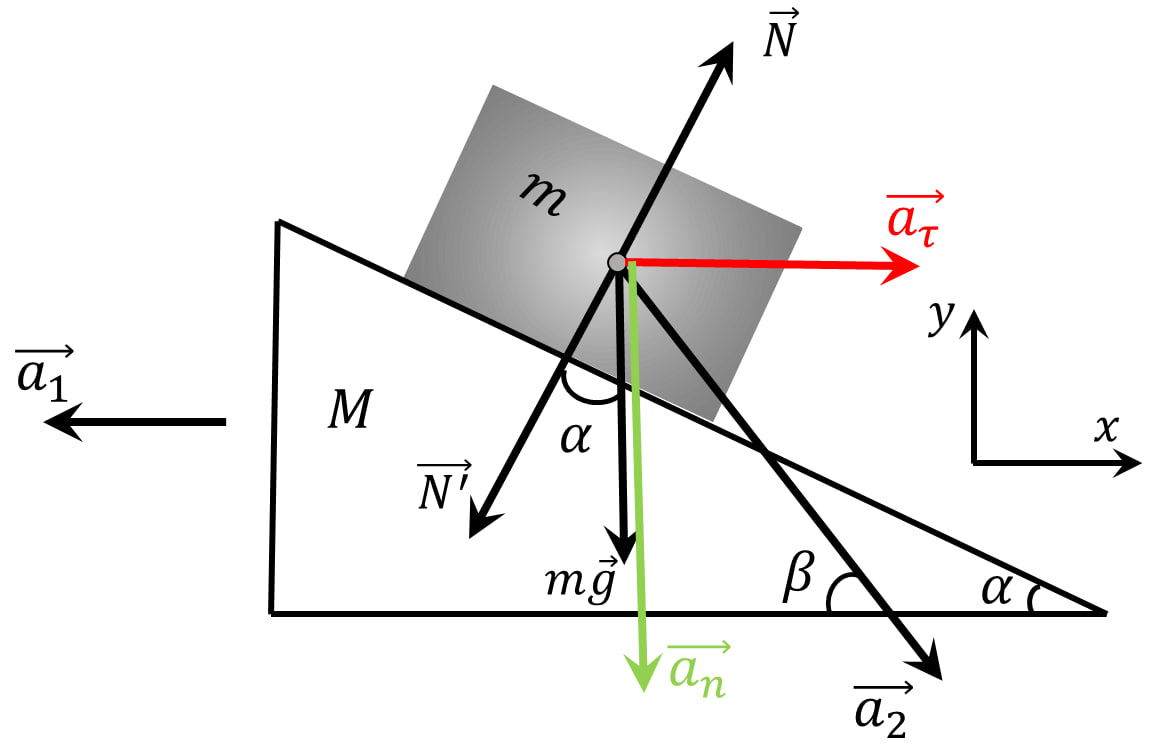
Из рисунка: $$a_n=a_2 \cdot \sin\beta$$ $$a_\tau =a_2 \cdot \cos\beta$$ $$a_n=a_\tau\cdot \tan\beta\quad(0)$$ Рассмотрим малое изменение координаты клина и бруска на нем за маленький промежуток $dt$: Клин сдвинулся на $dx_1$ Между тем, брусок в системе отсчета связанной с клином, по оси $OX$ брусок сдвинулся на $dx$, а по $OY$ — $dy$

Малое перещение за время $dt$

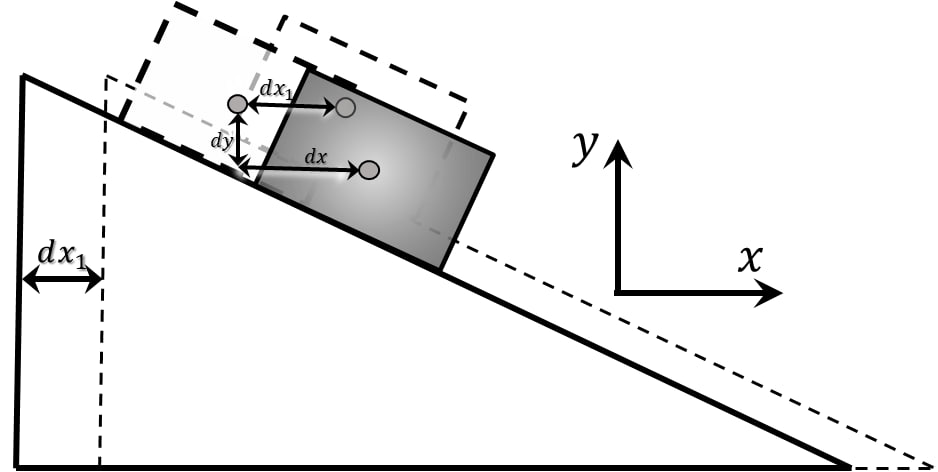
Относительно начальной точки, в СО Наблюдателя, брусок сдвинулся на $$OX: \;dx=dx_0+dx_1$$ $$OY: \;dy=dy_0$$ Т.к. брусок не отрывается, $$dy=dx \cdot \tan\alpha\quad(a)$$ Продеффиринцируем дважды обе части выражения $(a)$: $$\frac{dy}{d^2t} = \frac{dx}{d^2t} \cdot \tan\alpha$$ $$a_n = (a_\tau +a_1) \cdot \tan\alpha\quad(1)!$$ Запишем второй закон Ньютона для бруска на оси: $$OX: \;ma_\tau =N\,\sin\alpha\quad(2)$$ $$OY: \;ma_n=mg-N\cos\alpha\quad(3)$$ По третьему закону Ньютона Сила давления $\vec{N}{}'$ оказаная бруском на клин равна по модулю и проивоположна по направлению силе нормальной реакции опоры $\vec{N}$: $$\vec{N}{}'=-\vec{N}$$ Второй закон Ньютона для клина на оси $OX$: $$Ma_1=N\,\sin\alpha\quad(4)$$ Составим и решим систему уравнений $(0)$, $(1)$, $(2)$, $(3)$ и $(4)$ относительно $M$: $$\left\{\begin{matrix} a_n=a_\tau\cdot \tan\beta& \\ a_n = (a_\tau +a_1) \cdot \tan\beta& \\ ma_\tau =N\,\sin\alpha& \\ ma_n=mg-N\cos\alpha& \\ Ma_1=N\,\sin\alpha& \end{matrix}\right.$$ $$\left\{\begin{matrix} a_\tau\cdot \tan\beta = (a_\tau +a_1) \cdot \tan\alpha& \\ ma_\tau =N\,\sin\alpha& \\ ma_n=mg-N\cos\alpha& \\ Ma_1=N\,\sin\alpha& \end{matrix}\right.$$ $$M=ma_\tau\cdot \frac{1}{a_1}$$ $$a_\tau (\tan\beta -\tan\alpha ) = a_1\,\tan\alpha$$ $$\frac{a_\tau}{a_1} = \frac{\tan\alpha}{\tan\beta -\tan\alpha}$$ $$M=m \frac{a_\tau}{a_1}$$ $$\boxed{M=m \frac{\tan\alpha}{\tan\beta -\tan\alpha}}$$

Ответ:

$$M= m \frac{\tan\alpha}{\tan\beta -\tan\alpha}$$