$2.1.54.$ Электроны, движущиеся по окружности любого радиуса вокруг заряженной нити, имеют одну и ту же скорость $v$. Масса электрона $me$. Как зависит сила, действующая со стороны нити на электрон, от расстояния между электроном и нитью? Опишите качественно начальный отрезок траектории, по которой будет двигаться электрон, если скорость его при движении по окружности станет вдруг чуть меньше $v$? чуть больше $v$?
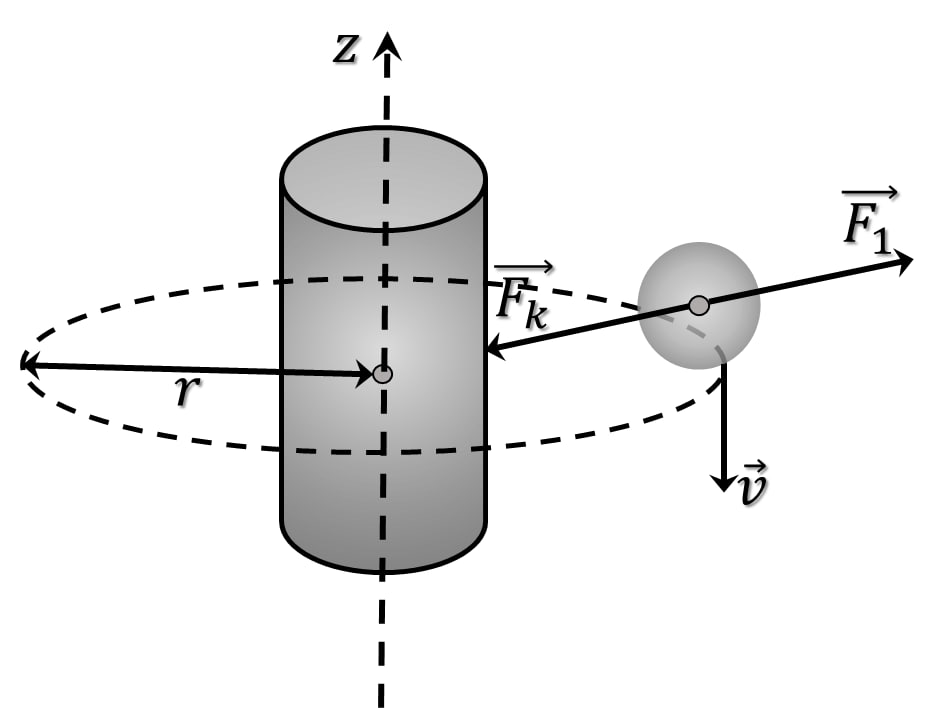
1. Стационарная круговая орбита электрона, представляющего собой отрицательно заряженную частицу с массой покоя $m_e$, будет иметь место в случае равенства по модулю кулоновской силы притяжения и силы инерции $$F_k=F_i$$ 2. Сила инерции прямо пропорциональна квадрату линейной скорости частицы и обратно пропорциональна расстоянию до оси вращения $$F_i=\frac{m_ev^2}{r}$$ Таким образом, сила Кулона в данном случае обратно пропорциональна расстоянию между электроном и заряженной нитью. 3. При увеличении заряда нити $$\boxed{F_k>\frac{m_ev^2}{r}}$$ для восстановления равновесия радиус орбиты должен уменьшится, при уменьшении заряда наоборот, радиус увеличится.
$$F = mev^2/r$$ Близки к параболам, касающимся окружности изнутри; снаружи.