$2.1.60^*.$ Из тонкого резинового жгута массы $m$ и жесткости $k$ сделали кольцо радиуса $R_0$. Это кольцо раскрутили вокруг его оси. Найдите новый радиус кольца, если угловая скорость его вращения равна $\omega$
Рассмотрим маленький кусочек жгута длины $dl = 2\alpha R$
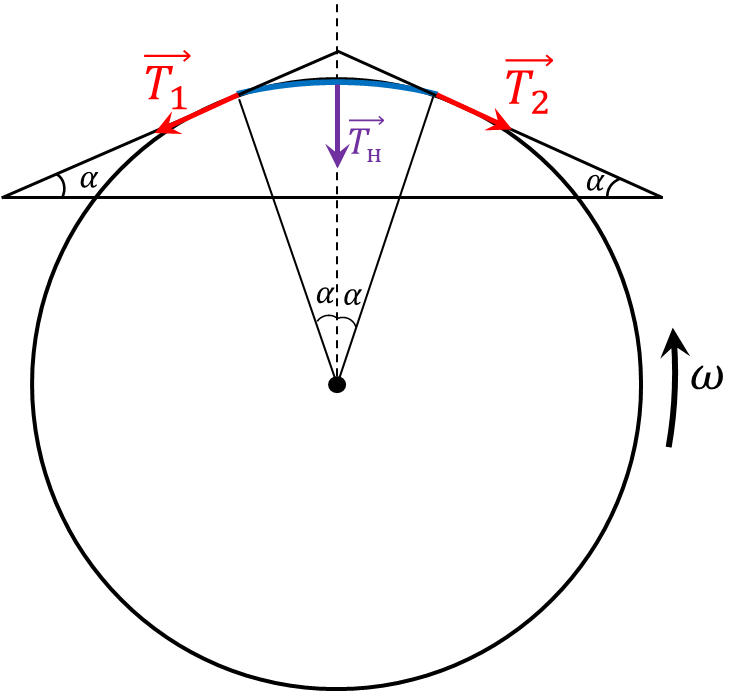
На кусочек жгута действуют силы натяжения $$T_1 = T_2 = 2k\alpha (R-R_0)$$ При учитывая $\sin\alpha\approx \alpha$ при малых углах $$T_{н} = 2T\alpha$$ В силу однородности жгута, кусочек длины $dl = 2\alpha R$ будет иметь массу $$dm = m \frac{\alpha}{\pi}$$ При этом на него будет действовать ценстростремительное ускорение $$a = \omega^2 R$$ Второй закон Ньютона запишем как $$dma = T_{н}$$ $$m \frac{1}{\pi} \omega^2 R = 4k (R-R_0)\alpha$$ Откуда находим $R$ $$\boxed{R = \frac{R_0}{1 − m \omega^2 /4 \pi^2 k}}$$ Анализируя полученное полученное выражение, при $R< R_0$ будет действовать результирующая сила упругости $\vec{T}_{н}$ направленная на расстяжение, которое не будет компенсировать центробежной силой. Таким образом, жгут будет бесконечно растягиваться и в конечном счёте разорвётся.
$R = R_0/(1 − m \omega^2 /4 \pi^2 k)$ при $\omega < 2\pi\sqrt{k/m};$
при $\omega\geq 2\pi\sqrt {k/m}$ кольцо неограниченно растягивается