$2.1.61^*.$ Кольцевая цепочка массы $m$ надета на горизонтальный диск радиуса $R$. Сила натяжения надетой цепочки $T$. Найдите коэффициент трения между диском и цепочкой, если при вращении диска с угловой скоростью, равной или превышающей $\omega$, цепочка с него спадает.
Для начала, советую ознакомиться с решением 2.1.60
Рассмотрим маленький кусочек жгута длины $dl = 2\alpha R$
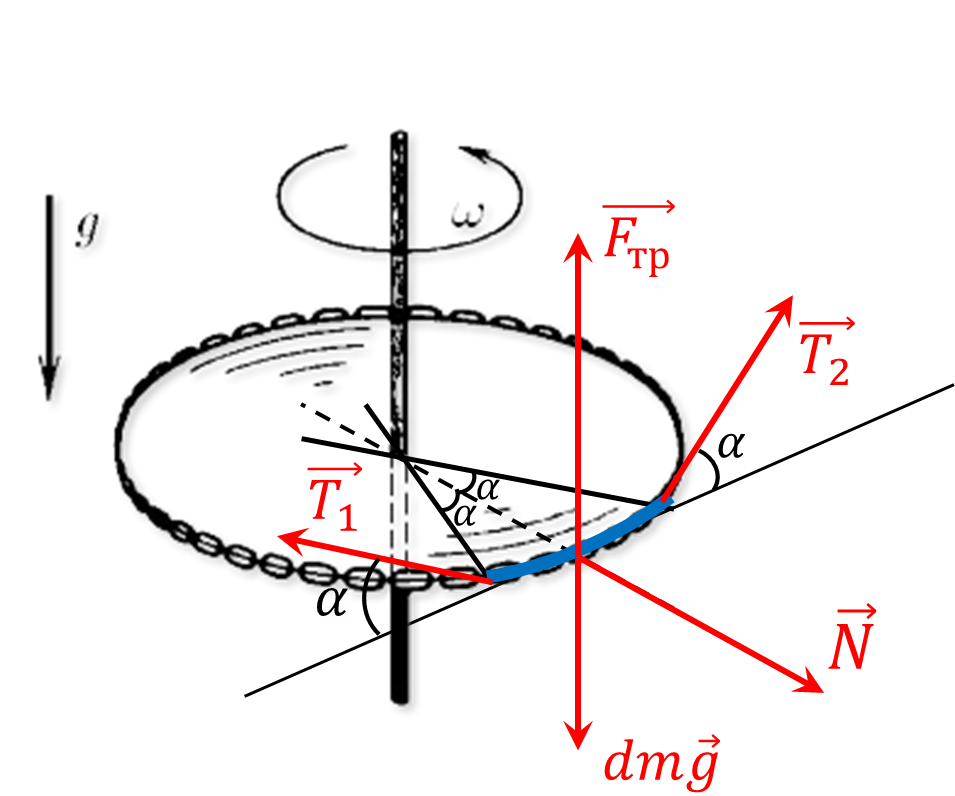
На кусочек жгута действует сила трения $\vec{F}_{тр}$ $$F_{тр} = \mu N$$ В силу однородности жгута, кусочек длины $dl = 2\alpha R$ будет иметь массу $$dm = m \frac{\alpha}{\pi}$$ При этом на него будет действовать ценстростремительное ускорение $$a = \omega^2 R$$ Второй закон Ньютона запишем как $$dma = N$$ $$m \frac{\alpha}{\pi} \omega^2 R = N$$ Откуда сила трения $$F_{тр} = \mu m \frac{\alpha}{\pi} \omega^2 R$$ Учитывая $\sin\alpha\approx \alpha$ при малых углах, запишем условие равновесия на вертикальную ось $$2T\alpha + F_{тр} = dm\,g$$ $$2T\alpha + \mu m \frac{\alpha}{\pi} \omega^2 R = mg \frac{\alpha}{\pi}$$ Откуда находим $\mu$ $$\boxed{\mu = \frac{mg}{2 \pi T - m \omega^{2} R}}$$
$$\mu = \frac{mg}{2 \pi T - m \omega^{2} R}$$