$2.1.64.$ С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая круг радиуса $R$, если коэффициент трения равен $\mu$? На какой угол от вертикали он должен при этом отклониться? Во сколько раз увеличится максимально допустимая скорость мотоциклиста при движении по наклонному треку с углом наклона $\alpha$ к горизонту по сравнению с максимально допустимой скоростью при движении по горизонтальному треку при том же радиусе поворота и том же коэффициенте трения?
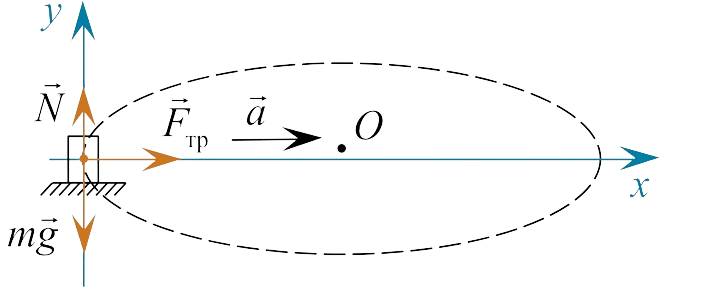
Изобразим силы, действующие на мотоцикл (см. рис. верхний), и запишем второй закон Ньютона $$\vec{N} + m\vec{g} + \vec{F}_{\text{тр}} = m\vec{a}.$$
В проекции на оси: $$Ox: \quad F_{\text{тр}} = ma;$$ $$Oy: \quad N - mg = 0.$$
Учитывая, что при движении по окружности $ a = \frac{v^2}{R} $, сила трения равна $ F_{\text{тр}} = \mu N $, получаем, что максимальная скорость движения мотоциклиста равна $$\boxed{v = \sqrt{\mu g R}}$$
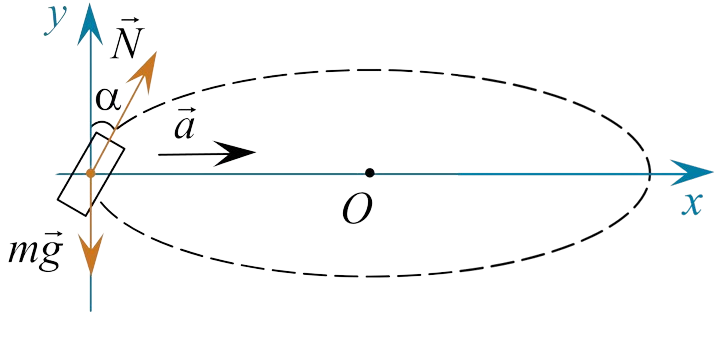
При повороте мотоциклист отклоняется к центру окружности на некоторый угол (см. рис. нижний). Тогда по второму закону Ньютона $$\vec{N} + m\vec{g} = m\vec{a}$$ $$Ox: \quad N \sin\beta = ma;$$ $$Oy: \quad N \cos\beta = mg.$$
Откуда $$\tan\beta = \frac{a}{g} = \frac{\mu g}{g}$$ $$\boxed{\beta = \arctan \mu}$$
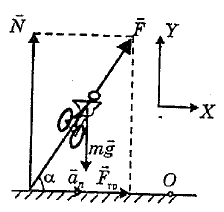
Рассмотрим движение велосипедиста по горизонтальному треку (рис.).
На велосипедиста действуют: сила тяжести $m \vec{g}$ и нормальная составляющая силы реакции опоры $\vec{N}$.
Центростремительное ускорение велосипедиста может сообщить здесь только сила трения покоя, направленная по радиусу окружности к центру $О$ и возникающая в том случае, когда велосипедист наклоняется к центру окружности.
Равнодействующая сил $\vec{N}$ и $\vec{F}_{тр} \Rightarrow \vec{F} = \vec{F}_{тр} + \vec{N}$ проходит через центр тяжести велосипедиста, и в противном случае существовал бы опрокидывающий момент сил.
По второму закону Ньютона для проекции на радиальное направление X $F_{тр} = ma_{n} = m \frac{v^{2}}{R}$, где $v$ - скорость движения велосипедиста.
Так как сила трения покоя $F_{тр} \leq \mu N = \mu mg$, то получаем неравенство $$m \frac{v^{2}}{R} \leq \mu mg$$ $$v^{2} \leq \mu gR \Rightarrow v \leq \sqrt{\mu gR}$$ максимальное значение скорости на горизонтальном треке $v_{1} = \sqrt{\mu gR}$.
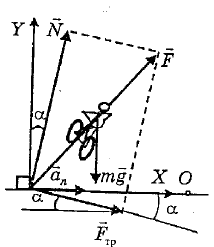
Рассмотрим движение велосипедиста по наклонному треку. Действующие на него силы изображены на рис. ($\vec{F}$ - равнодействующая сил реакции опоры $\vec{N}$ и силы трения покоя $\vec{F}_{тр}$). По второму закону Ньютона для проекций на оси X и Y:
по оси Y $N \cos\alpha - F_{тр} \sin\alpha - mg = 0$ (1)
по оси X $N \sin\alpha + F_{тр} \cos\alpha = ma_{n}$ (2), где $a_{n} = \frac{v^{2}}{R}$
($v$ - скорость движения по наклонному треку). Перепишем систему в виде: $$\begin{cases} N \cos\alpha - F_{тр} \sin\alpha = mg, (1') \\ N \sin\alpha + F_{тр} \cos\alpha = m \frac{v^{2}}{R} (2'). \end{cases}$$
Выразим из этой системы $N$ и $F_{тр}$. Для этого умножим уравнение $l'$ на $\cos\alpha$, а уравнение $(2')$ - на $\sin\alpha$: $$\begin{cases} N \cos^{2} \alpha - F_{тр} \sin\alpha = mg \cos\alpha , \\ N \sin^{2} \alpha + F_{тр} \cos\alpha\sin\alpha = m \frac{v^{2}}{R} \sin\alpha . \end{cases}$$
После сложения получим $$N(\cos^{2} \alpha + \sin^{2} \alpha ) = mg \cos\alpha + m \frac{v^{2}}{R} $$ $$N = m \left ( g \cos\alpha + \frac{v^{2}}{R} \right )$$
Умножим $(1')$ на $\sin\alpha$, а $(2')$ - на $\cos\alpha$, тогда $$\begin{cases} N \cos^{2} \alpha - F_{тр} \sin\alpha = mg \cos\alpha , \\ N \sin^{2} \alpha + F_{тр} \cos\alpha\sin\alpha = m \frac{v^{2}}{R} \sin\alpha . \end{cases}$$
После вычислений найдем $$F_{тр} = \left ( \frac{v^{2}}{R} - g \sin\alpha\right )$$ Так как $F_{тр}$ - сила трения покоя, то $$F_{тр} \leq \mu N \Rightarrow m \left ( \frac{v^{2}}{R} \cos\alpha - g \sin\alpha\right ) \leq \mu m \left ( g \cos\alpha + \frac{v^{2}}{R} \sin\alpha\right )$$ $$ \frac{v^{2}}{R} ( \cos\alpha - \mu\sin\alpha ) \leq g ( \mu\cos\alpha + \sin\alpha )$$ Разделим обе части на $\cos\alpha$ (из условия $\cos\alpha > 0$). $$\frac{v^{2}}{R} (1 - \mu \tan\alpha ) \leq g( \mu + \tan\alpha )$$
Если $(1 - \mu \tan\alpha ) > 0$, то $v^{2} \leq \frac{gR( \mu + \tan\alpha )}{1 - \mu \tan\alpha}$, или $v \leq \sqrt{ \frac{gR( \mu + \tan\alpha )}{1 - \mu \tan\alpha}}$
Значит максимальная скорость при движении по наклонному треку $$v_{2} = \sqrt{ \frac{gR ( \mu + \tan\alpha )}{1 - \mu \tan\alpha}}$$
Отношение $$\boxed{\frac{v_{2}}{v_{1}} = \sqrt{ \frac{ \mu + \tan\alpha}{ \mu (1 - \tan\alpha )}}}$$
$$v=\sqrt{\mu gR}$$ $$\beta =\arctan \mu$$ $$\frac{u}{v}=\sqrt{\frac{\mu +\operatorname{tg}\alpha}{\mu (1-\mu\operatorname{tg}\alpha )}}$$