$2.1.67^*.$ С какой угловой скоростью должен вращаться вокруг своей оси горизонтально расположенный цилиндр, чтобы мелкие частицы внутри цилиндра не соскальзывали с его поверхности? Коэффициент трения между поверхностью цилиндра и частицами равен $1$, внутренний радиус цилиндра $R$.
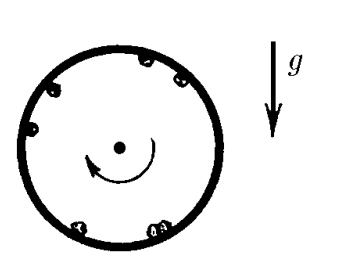
По второму закону Ньютона имеем $$m \omega^{2}r = N + mg \sin\alpha$$ где $N$ — сила нормального давления.
Чтобы не было проскальзывания, должно выполняться условие $$mg \cos\alpha\leq k(m \omega^{2} r - mg \sin\alpha )$$ откуда
$\omega^{2} \geq \frac{g}{r} ( \cos\alpha + \sin\alpha )$ при $k=l$.
Таким образом, $$\boxed{\omega_{min} = \sqrt{\sqrt{2} g/r}}$$
$$\omega_{min} = \sqrt{\sqrt{2} g/r}$$