$2.2.15.$ При $\beta$-распаде покоящегося первоначально нейтрона образуются протон, электрон и нейтрино. Импульсы протона и электрона $p_1$ и $p_2$, угол между ними $\alpha$. Определите импульс нейтрино
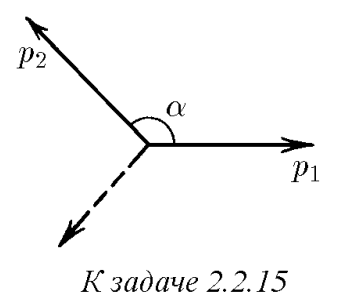
Запишем закон сохранения импульса: $\vec p_1 + \vec p_2 +\vec p_3 = 0$ по т. косинусов сложим $p_1$ и $p_2$: $|\vec p_1 + \vec p_2| $$= \sqrt{{p_1}^2+{p_2}^2 -2p_1p_2\cos (\pi - \alpha )} $ $|\vec p_1 + \vec p_2| $$= \sqrt{{p_1}^2+{p_2}^2 + 2p_1p_2\cos (\alpha )}$ угол берём $\pi - \alpha$ так как при сложении угол будет смежный с $\alpha$