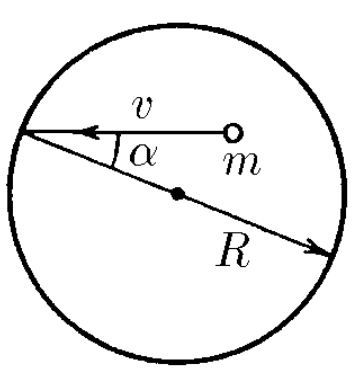
$2.2.33^*.$ Внутри сферы радиуса $R$ со скоростью $v$ движется частица массы $m$, упруго ударяясь о ее стенки. Скорость частицы образует угол $\alpha$ с радиусом, проведенным в точку удара. Какова по модулю средняя сила, действующая со стороны стенок сферы на частицу? Какова средняя сила, действующая на единицу площади сферы, если в единице объема содержится $N$ таких частиц? Частицы между собой не сталкиваются.
Импульс, который передает частица найдем как $$dp = 2mv\cos\alpha$$ Путь, который пройдет частица между двумя последовательными ударами $$x = 2R\cos\alpha$$ Таким образом время между двумя последовательными ударами $$dt = \frac{x}{v} = \frac{2R\cos\alpha}{v}$$ Запишем второй закон Ньютона в импульсной форме $$F = \frac{dp}{dt} = 2mv\cos\alpha\frac{v}{2R\cos\alpha}$$ $$\boxed{F = \frac{mv^2}{R}}$$ Количество частиц в единице объема обозначим за $N$, тогда количество частиц в сфере радиуса $R$ составляет $$n = \frac{4}{3} \pi r^3 N \quad\text{(1)}$$ Общая сила действующая на стенки сферы: $$F = n\frac{mv^2}{R} \quad\text{(2)}$$ А давление по определию - сила, действующая на единицу площади $$ p = \frac{F}{4\pi R^2} $$ Подставляем $\text{(1)}$ и $\text{(2)}$ $$ p = \frac{4}{3} \pi r^3 N \frac{mv^2}{4\pi R^3} $$ $$\boxed{p = \frac{Nmv^2}{3}}$$
$$F = \frac{mv^2}{R}$$ $$p = F/S = \frac{Nmv^2}{3}$$