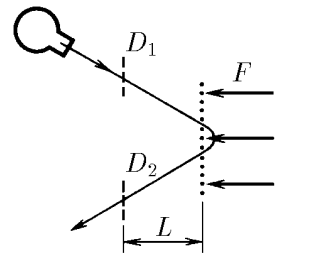
$2.2.4.$ В масс-пролетном спектрометре источник испускает сгусток заряженных частиц, которые сначала летят свободно и пролетают через первый датчик $D_1$, находящийся на расстоянии $L$ от сетки. За сеткой по нормали к ней на частицы действует электрическая сила $F$. Частицы поворачиваются и вылетают через сетку назад, пролетая через второй датчик $D_2$, находящийся на том же расстоянии от сетки. От напряжения источника зависит скорость вылетающих частиц, но точное ее значение остается неизвестным. Меняя напряжение, измеряют время между срабатываниями датчиков и находят наименьшее его значение $\Delta t$. Какова масса частицы? Как можно найти массу частиц, если источник испускает несколько сортов частиц с разной массой?
Время пролета расстояния $2L$ $$t_1 = \frac{2L}{v_0}$$
Время разворота частицы $$t_2 = 2\frac{mv_0}{F}$$
$$t(v) = \frac{2L}{v_0} + 2\frac{mv_0}{F}$$ Находим производную времени по скорости и ищем экстремум(из условия минимума $\Delta t$) $$t'(v) = 2\frac{m}{F} - \frac{2L}{{v_0}^2} = 0 $$
отсюда
$v_0 = \sqrt{\frac{FL}{m}}$
тогда
$$t_1 =t_2 = 2\sqrt{\frac{mL}{F}}, $$ $$\Delta t = 4\sqrt{\frac{mL}{F}}$$ $$\Delta t = 4\sqrt{\frac{mL}{F}} \Rightarrow \boxed{m = \frac{F{\Delta t}^2}{16L}}$$
$$m=\frac{F{\Delta t}^2}{16L}$$