$2.2.46^*.$ Газ, вытекающий из сопла ракеты, имеет скорость $v$ относительно нее. Определите изменения скорости ракеты после того, как ее масса из-за истечения газа уменьшилась в $n$ раз.
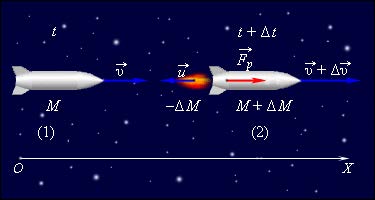
Запишем закон сохранения импульса за малый промежуток времени $$Mv = (M+dm)(v+dv) - dm(v+u)$$ $$Mv = Mv + dmu + mdv$$ $$dmu = -mdv$$ Откуда получаем соотношение $$-\frac{dm}{m} = \frac{dv}{u}$$ Интегрируем обе части уравнения $$-\int_{M_1}^{M_2}\frac{dm}{m} = \int_{v_1}^{v_2}\frac{dv}{u}$$ $$\boxed{\ln \frac{M_1}{M_2} = \frac{\Delta{v}}{u}}$$ Это уравнение называется формулой Циалковского
Откуда получаем искомое соотношение $$\boxed{u = v \ln n}$$
$$u = v \ln n$$