$2.2.47^*.$ Скорость газа, выбрасываемого ракетой, относительно нее равна $u=2 \text{ км/с}$. Оцените начальную массу ракеты, которая может вывести на орбиту Земли спутник массы $M_2=10^4 \text{ кг}$. Как изменится результат при вдвое большей скорости истечения газа?
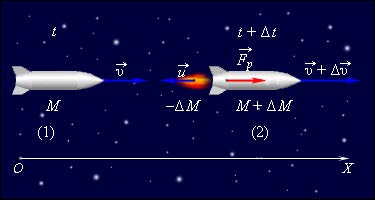
Запишем закон сохранения импульса за малый промежуток времени $$Mv = (M+dm)(v+dv) - dm(v+u)$$ $$Mv = Mv + dmu + mdv$$ $$dmu = -mdv$$ Откуда получаем соотношение $$-\frac{dm}{m} = \frac{dv}{u}$$ Интегрируем обе части уравнения $$-\int_{M_1}^{M_2}\frac{dm}{m} = \int_{v_1}^{v_2}\frac{dv}{u}$$ $$\boxed{\ln \frac{M_1}{M_2} = \frac{\Delta{v}}{u}} \quad\text{(1)}$$ Это уравнение называется формулой Циалковского
Чтобы вывести тело на орбиту, ему необходимо задать первую космическую скорость $$v = \Delta v = \sqrt{G\frac{M}{R}} = 7.9 \text{ км/с}$$ Подставляем в $\text{(1)}$ и получаем $M_2$ $$M_1 = M_2 e^{\frac{v}{u}} = 5.2 \cdot 10^5 \text{ кг}$$
$m \approx 5.5 \cdot 10^5 \text{ кг};$ в $7.4$ раза меньше