$2.3.1.$ Пучок заряженных частиц различной массы, имеющих одну и туже скорость $v$, направили по нормали к двум сеточным электродам, между которыми на каждую частицу действует одна и та же сила $F$. При какой наименьшей массе частиц в пучке все они достигнут второй сетки, если ширина зазора между электродами равна $l$?
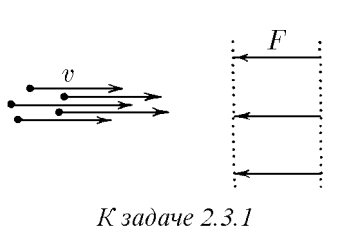
По условию задачи требуется найти наименьшую массу частиц в пучке при которой все они достигнут второй сетки. Тогда работа силы между сеточными электродами на расстоянии $l$ равна изменению кинетической энергии частиц $Fl = \Delta E_k = \frac{mv^2}{2}$, здесь учтено, что работа силы $F$ отрицательна, а изменение кинетической энергии $\Delta E_k = 0 - \frac{mv^2}{2}$ Тогда минимальная масса частиц $m = \frac{2Fl}{v^2}$. Примечание: задачу можно решить динамически, через импульс силы. Попробуйте самостоятельно прийти к ответу.