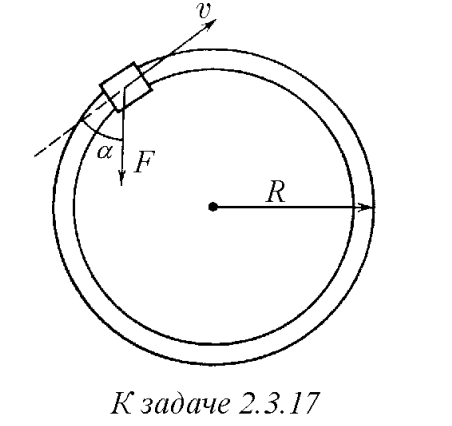
$2.3.17.$ По рельсам, образующим горизонтальный круговой путь радиуса $R$, катится со скоростью $v$ вагонетка массы $m$. Рабочий бежит за ней и начинает останавливать ее, натягивая привязанный к вагонетке трос с силой $F$ под углом $\pi − \alpha$ к направлению скорости вагонетки. Сколько оборотов по кругу совершит вагонетка до остановки? Трением пренебречь.
Вагонетка остановится, когда вся кинети ческая энергия будет израсходована на работу силы $F$. причём пройденный до остановки путь будет являться верхним пределом интеграла работы. $\frac{mv^2}{2}=F\cos\alpha\cdot \int_{0}^{2\pi nR}dr$ $\frac{mv^2}{2}=F\cos\alpha\cdot 2\pi nR$ $n=\frac{mv^2}{4 F\cos\alpha\cdot \pi R}$ где $n$ — полное число оборотов вагонетки до остановки.