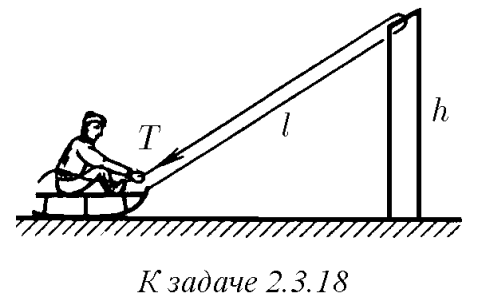
$2.3.18^*.$ Веревка привязана к санкам и переброшена через перекладину ворот высоты $h$. Мальчик, сидящий на санках, начинает выбирать веревку, натягивая ее с силой $T$. Какую скорость он приобретет, проезжая под перекладиной? Начальная длина натянутой части веревки $2l$, масса мальчика с санками $m$. Трением пренебречь.
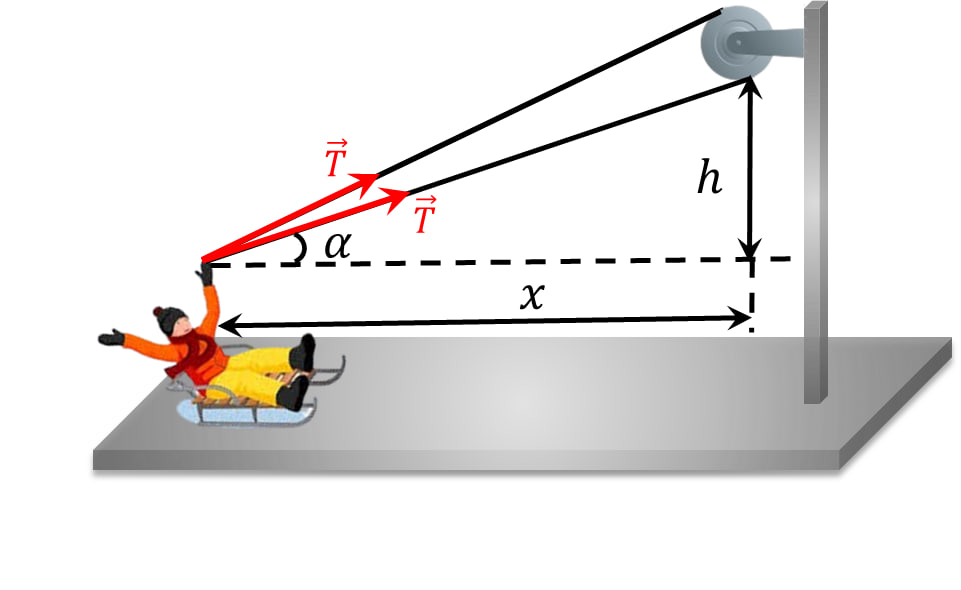
На санки действует единственная внешняя сила $2\vec{T}$, направленная под углом $\alpha$ к горизонту $F_x=2T\cos\alpha$ Из рисунка: $\cos\alpha =\frac{x}{\sqrt{x^2+h^2}}$ Тогда $F_x=T\frac{2x}{\sqrt{x^2+h^2}}$ Работа внешней силы равна: $A=\int_{0}^{x_0}F_xdx$ $A=2T\int_{0}^{x_0}\frac{x}{\sqrt{x^2+h^2}}dx\quad(a)$ $\int\frac{x}{\sqrt{x^2+h^2}}dx=\sqrt{x^2+h^2}+C$ $\int_{0}^{x_0}\frac{x}{\sqrt{x^2+h^2}}dx=\sqrt{x_0^2+h^2}-h$ По условию: $L=\sqrt{x^2+h^2}$ Тогда $(a)$ можно переписать: $A=2T(L-h)$ Энергия внешней силы перешла в кинетическую энергию санок: $A=E_{кин}$ $2T(L-h)=\frac{mv^2}{2}$ Отсюда: $v=\sqrt{\frac{4T(L-h)}{m}}$