$2.3.48^*.$ На горизонтальной плоскости лежат два бруска массы $m_1$ и $m_2$, соединенных недеформированной пружиной. Определите, какую наименьшую постоянную силу нужно приложить к левому бруску, чтобы сдвинулся и правый, если коэффициент трения грузов о плоскость $\mu$.
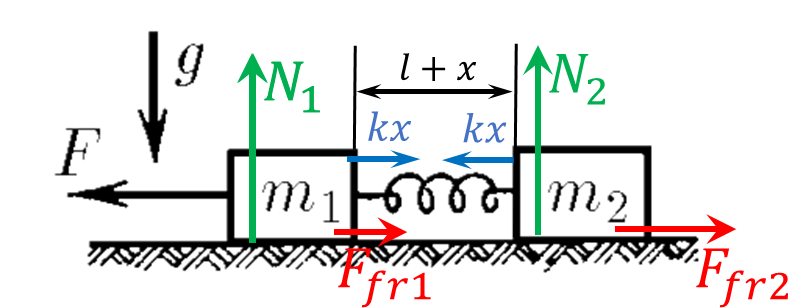
Условие равновесия на горизонтальную ось $$ F_\text{fr1} = \mu N_1 \quad (1) $$ $$ F_\text{fr2} = \mu N_2 \quad (2) $$ Альтернативно, для вертикальной оси $$ N_1 = m_1g \quad (3) $$ $$ N_2 = m_2g \quad (4) $$ Подставляем $(3)$ и $(4)$ в уравнения $(1)$ и $(2)$ $$ F_\text{fr1} = \mu m_1g $$ $$ F_\text{fr2} = \mu m_2g $$ Воспользуемся законом сохранения энергии: сила $\vec{F}$ действует против силы натяжения пружины и против силы трения. $$ A=Fx=\Delta E $$ Подставляя потенциальную энергию пружины $$ Fx = \frac{kx^2}{2} + F_\text{fr1}x $$ $$ F= \frac{kx}{2} + \mu m_1 g \quad (5) $$ Из состояния равновесия в установившемся состоянии $$ kx = \mu m_2 g \quad (6) $$ После подстановки $(6)$ в $(5)$ мы наконец получаем $$ \boxed{ F = \mu g \left( m_1 +\frac{m_2}{2} \right)} $$
$$F = \mu g \left( m_1 +\frac{m_2}{2}\right) $$