$2.3.6.$ Однородный брусок, скользящий по гладкой горизонтальной поверхности, попадает на шероховатый участок этой поверхности ширины $L$, коэффициент трения о который $\mu$. При какой начальной скорости он преодолеет этот участок?
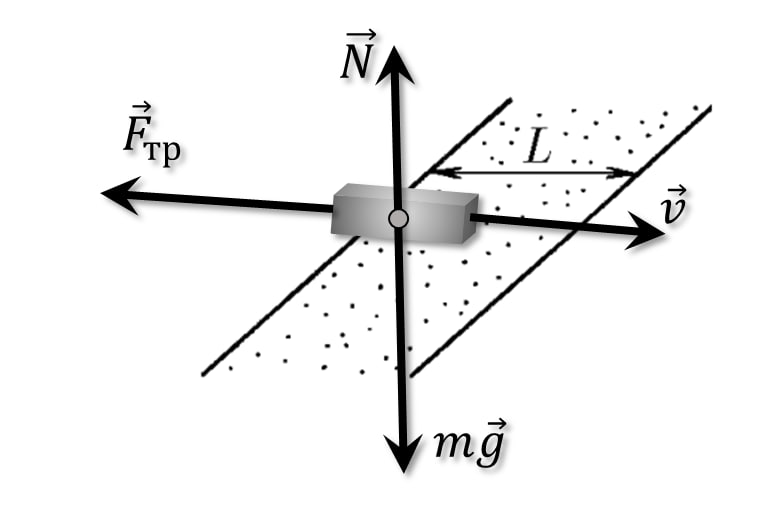
На брусок действует постоянная сила трения скольжение $\vec{F}_{тр}$: $\vec{F}_{тр}=\mu\vec{N}$ $\vec{F}_{тр}=\mu m\vec{g}$ Из закона сохранения механической энергии: $F_{тр} x = \frac{mv_0^2}{2}-\frac{mv^2}{2}$ $\mu m g x = \frac{mv_0^2}{2}-\frac{mv^2}{2}$ $\mu g x = \frac{v_0^2}{2}-\frac{v^2}{2}$ $v = \sqrt{v_0^2-2\mu g x}$ Где $v_0$ – начальная скорость Тело остановится если $v=0$: $\sqrt{v_0^2-2\mu g x} = 0$ $v_0^2=2\mu g x$ Т.е. тело остановится на расстоянии $x$: $x=\frac{v_0^2}{2\mu g }$ Условие прохождение полосы: $x\geq L$ $\frac{v_0^2}{2\mu g } \geq L$ $ v_0 \geq \sqrt{2\mu gL}$