$2.3.8.$ Пружина жесткости $k$ прикреплена одним концом кнеподвижнойстенке. На другой ее конец вдоль пружины с начальной скоростью $v$ налетает шар массы $m$. Какова наибольшая деформация сжатия пружины? Ответьте на этот же вопрос для случая, когда пружина предварительно сжата и удерживается нерастяжимой нитью, связывающей ее концы (начальная деформация пружина равна $x_0$)
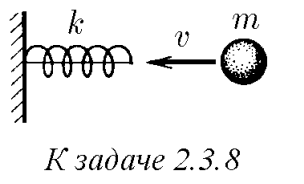
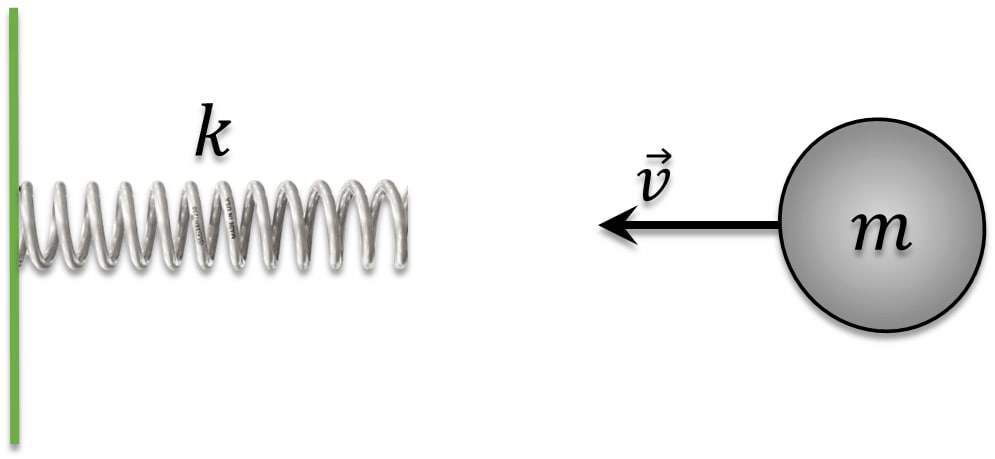
Т.к. пружина закреплена, из закона сохранения энергии, энергия сжатой пружины равна начальной кинетической энергии шарика: $E_{кин}=E_{пр}$ $\frac{mv^2}{2}=\frac{kx^2}{2}$ $x=v\sqrt{\frac{m}{k}}\quad(a)$
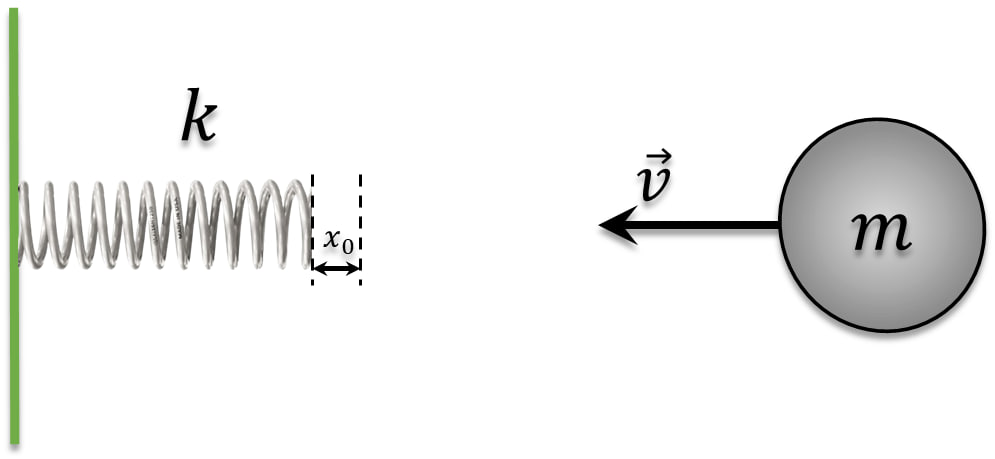
Для случая $2$ пружина изначально имеет некоторую начальную энергию $\frac{kx_0^2}{2}$: $E_{кин}=E_{пр}$ $\frac{kx^2}{2}-\frac{kx_0^2}{2}=\frac{mv^2}{2}$ $x^2=x_0^2+\frac{m}{k}v^2$ $x=\sqrt{x_0^2+\frac{m}{k}v^2}$ Заметим, что при $x_0=0$, мы получаем выражение $(a)$