$2.7.24.$ Ознакомьтесь с условиями задачи 2.4.18. При какой начальной угловой скорости обруч радиуса $R$ вернется в исходную точку, двигаясь с постоянным ускорением по горизонтальному полу? На чальная скорость центра обруча $v$.
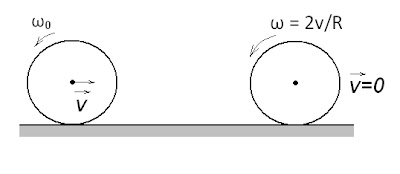
Поскольку обруч возвращается в начальное место - место старта, то его конечная скорость равна начальной: $v_к=v_н-v$ Из второго закона Ньютона для вращательного движения имеем: $M=I\beta$ $μmgR = mR^2(\omega_0 – \omega )/t $ $μgt = R(\omega_0 – 2v/R) \quad(1)$ Из второго закона Ньютона для поступательного движения получим: $F_т = ma$ $μmg = mv/t$ $μgt = v \quad(2)$ Из формул $(1)$ и $(2)$ находим: $\omega_0 = 3v/R$ а искомое условие будет иметь вид $\omega_0 \geq 3v/R$