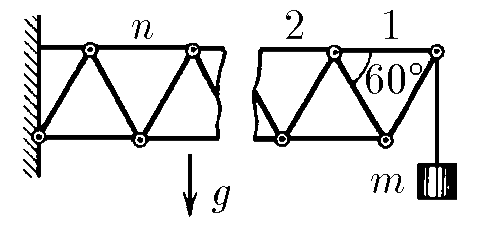
$2.8.25^*.$ К системе из одинаковых стержней, соединенных шарнирами, подвешен груз массы $m$, как показано на рисунке. Определите силу, растягивающую $n$-й верхний горизонтальный стержень
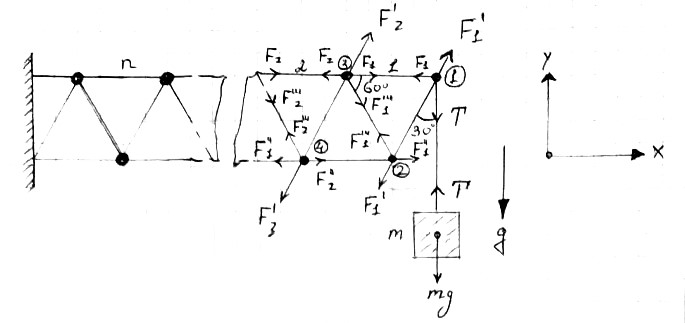
Рассмотрим силы, действующие на 1-й стержень. $$ \left\{\begin{matrix} F_1=F_1'\cos(60^{\circ})=F_1'/2 \\ T=F_1'\cos(30^{\circ})=\sqrt{3}F_1'/2 \end{matrix}\right. $$ $$ \left\{\begin{matrix} F_1'''\cos(30^{\circ})=F_1'\cos(30^{\circ}) \\ F_1'=F_1'''\\ F_1'''\cos(60^{\circ})+F_1'\cos(60^{\circ})=F_1'' \\ F_1'=F_1''\\ \end{matrix}\right. $$ Аналогично для второго стержня $$ \left\{\begin{matrix} F_2''\cos(30^{\circ})=F_1'''\cos(30^{\circ}) \\ F_2'=F_1'''=F_1'\\ F_2=F_2'\cos(60^{\circ})+F_1+F_1'''\cos(60^{\circ})\\ F_2=3F_1'/2 \end{matrix}\right. $$ $$ F_1'=\frac{2T}{\sqrt{3}}=\frac{2mg}{\sqrt{3}} $$ $$ \boxed{F_1=\frac{mg}{\sqrt{3}} \to F_2=\frac{3mg}{\sqrt{3}}} $$ Как мы видим, индекс при $F_2$ увеличился на два, что приводит к рекуррентному соотношению для индекса $n$-го стержня: $2n-1$ $$ \boxed{F_n=\frac{(2n-1)mg}{\sqrt{3}}} $$
$$T_n=(2n-1)mg/\sqrt{3}$$